Tập hợp SVIP

1. TẬP HỢP VÀ PHẦN TỬ CỦA TẬP HỢP

Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định. Các đối tượng ấy được gọi là những phần tử của tập hợp đó.

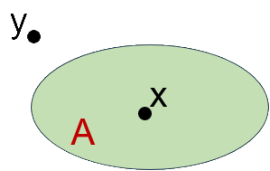
⚡$x$ là một phần tử của tập $A$, kí hiệu $x \in A$ (đọc là $x$ thuộc $A$). 

⚡$y$ không là phần tử của tập $A$, kí hiệu là $y \notin A$ (đọc là $y$ không thuộc $A$).

Chú ý: 

+ Người ta thường đặt tên tập hợp bằng chữ cái in hoa.

+ Khi $x$ thuộc $A$, ta còn nói "$x$ nằm trong $A$" hay "$A$ chứa $x$".

 Ví dụ 1: Gọi C là tập hợp các chữ cái trong từ "TẬP HỢP".

Khi đó T $\in$ C, M $\notin$ C.

2. MÔ TẢ MỘT TẬP HỢP

a. Hai cách mô tả một tập hợp 

Cách 1: Liệt kê các phần tử của tập hợp, tức là viết các phần tử trong dấu ngoặc { } theo thứ tự tùy nhưng mỗi phần tử chỉ được viết một lần.

Ví dụ: Với tập P gồm các số 0; 1; 2; 3; 4; 5, ta viết: 

P = {0; 1; 2; 3; 4; 5}.

Cách 2: Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp.

Ví dụ: Với tập P = {0; 1; 2; 3; 4; 5} ta cũng có thể viết:

P = {$n$ | $n$ là một trong sáu số tự nhiên đầu tiên}.

b. Tập rỗng

Tập hợp không chứa phần tử nào gọi là tập rỗng, kí hiệu là $\varnothing$.

Ví dụ: tập hợp những người sống trên Mặt Trăng là tập rỗng. 

Ví dụ 2: Gọi $\mathbb{N}$ là tập hợp các số tự nhiên. Ta có thể viết tập  $\mathbb{N}$  như sau: 

+ Liệt kê các phần tử: $\mathbb{N}=\{0; \, 1; \, 2; \, 3; \, ...\}$.

+ Nêu dấu hiệu đặc trưng cho các phần tử: $\mathbb{N} = \{m \Big| m$ là một số tự nhiên$\}$.