Tập hợp các số nguyên SVIP

I. TẬP HỢP \(ℤ\) CÁC SỐ NGUYÊN

- Số tự nhiên khác 0 còn được gọi là số nguyên dương.

- Các số nguyên âm, số 0 và các số nguyên dương tạo thành tập hợp các số nguyên.

- Tập hợp các số nguyên được kí hiệu là \(ℤ\).

Chú ý: 

- Số 0 không phải số nguyên âm, cũng không phải số nguyên dương.

- Các số nguyên dương 1, 2, 3, ... đều mang dấu "\(+\)" nên còn được viết là \(+1,+2,+3\), ...

Ví dụ: Số nào là số nguyên, số nào không là số nguyên trong các số sau: \(-\)9; 0; \(\dfrac{3}{4}\); 7; 9,6? 

Giải

Các số \(-\)9; 0; 7 là số nguyên; các số \(\dfrac{3}{4}\); 9,6 không là số nguyên.

Ví dụ: Xác định tính đúng sai của mỗi phát biểu sau:

a) Mỗi số tự nhiên đều là số nguyên;

b) Mỗi số tự nhiên đều là số nguyên dương.

Giải

a) Đúng

b) Sai

II. BIỂU DIỄN SỐ NGUYÊN TRÊN TRỤC SỐ

Ta có thể biểu diễn số nguyên trên trục số. Có hai loại trục số như sau:

a) Trục số nằm ngang (Hình 1) có:

• Chiều dương hướng từ trái sang phải (được đánh dấu bằng mũi tên);
• Điểm gốc của trục số là điểm 0 (điểm biểu diễn số 0);
• Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm 0 với điểm 1 (biểu diễn số 1 và nằm bên phải điểm 0).

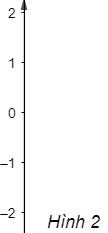
b) Trục số thẳng đứng (Hình 2) có:

• Chiều dương hướng từ dưới lên trên (được đánh dấu bằng mũi tên);
• Điểm gốc của trục số là điểm 0 (biểu diễn số 0);
• Đơn vị đo độ dài trên trục số là một đoạn thẳng nối điểm 0 với điểm 1 (biểu diễn số 1 và nằm phía trên điểm 0).

Trên trục số nằm ngang, điểm biểu diễn số nguyên âm nằm bên trái điểm 0, điểm biểu diễn số nguyên dương nằm bên phải điểm 0.

Trên trục số thẳng đứng, điểm biểu diễn số nguyên âm nằm phía dưới điểm 0, điểm biểu diễn số nguyên dương nằm phía trên điểm 0.

Ví dụ: Trên trục số ở Hình 3, điểm A biểu diễn số \(-2\), điểm B biểu diễn số 3.

Quan sát Hình 3 và trả lời các câu hỏi:

a) Điểm C biểu diễn số nào?

b) Điểm nào biểu diễn số \(-4\)?

c) Điểm nào biểu diễn số 5?

Giải

a) Điểm C biểu diễn số 1.

b) Điểm D biểu diễn số \(-4\).

c) Điểm E biểu diễn số 5.

Chú ý: Khi nói "trục số" mà không giải thích gì thêm, ta hiểu là nói về trục số nằm ngang.

III. SỐ ĐỐI CỦA MỘT SỐ NGUYÊN

Trên trục số, hai số nguyên (phân biệt) có điểm biễu diễn nằm về hai phía của gốc 0 và cách đều gốc 0 được gọi là hai số đối nhau.

Số đối của 0 là 0.

Ví dụ: Tìm số đối của các số sau: \(-12,-9,0,3,17\).

Giải

Số đối của các số \(-12,-9,0,3,17\) lần lượt là: \(12,9,0,-3,-17\).

IV. SO SÁNH CÁC SỐ NGUYÊN

1. So sánh hai số nguyên

Trên trục số nằm ngang, nếu điểm \(a\) nằm bên trái điểm \(b\) thì số nguyên \(a\) nhỏ hơn số nguyên \(b\).

Trên trục số thẳng đứng, nếu điểm \(a\) nằm phía dưới điểm \(b\) thì số nguyên \(a\) nhỏ hơn số nguyên \(b\).

Nếu \(a\) nhỏ hơn \(b\) thì ta viết \(a< b\) hoặc \(b>a\).

Ví dụ: Biểu diễn các số \(-2\) và \(3\) trên trục số nằm ngang. Từ đó so sánh các cặp số sau: \(-2\) và 0; 3 và 0.

Giải

Ta có: 

Điểm \(-2\) nằm bên trái điểm 0 nên \(-2< 0\).

Điểm 3 nằm bên phải điểm 0 nên \(3>0\).

Lưu ý:

Số nguyên dương luôn lớn hơn 0. Số nguyên âm luôn bé hơn 0.

Ví dụ: Quan sát trục số sau:

Dùng kí hiệu "\(< \)", "\(>\)" để biểu diễn quan hệ giữa các cặp số nguyên: \(a\) và \(b\), \(b\) và \(c\), \(a\) và \(c\).

Giải

Ta có: \(a< b,b< c\) và \(a< c\).

Lưu ý:

Nếu \(a< b\) và \(b< c\) thì \(a< c\).

2. Cách so sánh hai số nguyên

Số nguyên âm luôn nhỏ hơn số nguyên dương.

Để so sánh hai số nguyên âm, ta làm như sau:

     Bước 1. Bỏ dấu "\(-\)" trước cả hai số âm

     Bước 2. Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên dương ban đầu (trước khi bỏ dấu "\(-\)") sẽ lớn hơn.

Ví dụ: So sánh \(-215\) và \(-304\).

Giải

Bỏ dấu "\(-\)" trước các số \(-215\) và \(-304\), ta được các số lần lượt là \(215\) và \(304\).

Do \(215< 304\) nên \(-215>-304\).