Tính đồng biến, nghịch biến của hàm số SVIP

Hoàn thành các khẳng định sau:

⭕ Hàm số $y=f(x)$ gọi là

$\forall x_1, \, x_2\in\left(a;b\right):x_1< x_2\Rightarrow$ $f(x_1) < f(x_2)$;

⭕ Hàm số $y=h(x)$ gọi là

$\forall x_1, \, x_2\in\left(a;b\right):x_1< x_2\Rightarrow$ $h(x_1) > h(x_2)$.

Cho hàm số $f\left( x \right)=4-3x$. Khẳng định nào sau đây đúng?

Xét tính đồng biến, nghịch biến của hàm số $f\left( x \right)=\dfrac{3}{x}$ trên khoảng $\left( 0;+\infty \right)$. Khẳng định nào sau đây đúng?

Xét tính đồng biến, nghịch biến của hàm số $f\left( x \right)=x+\dfrac{1}{x}$ trên khoảng $\left( 1;+\infty \right)$. Khẳng định nào sau đây đúng?

Xét tính đồng biến, nghịch biến của hàm số $f\left( x \right)={{x}^{2}}-4x+5$ trên khoảng $\left( -\infty ;2 \right)$ và trên khoảng $\left( 2;+\infty \right)$. Khẳng định nào sau đây đúng?

Xét tính đồng biến, nghịch biến của hàm số $f\left( x \right)=\dfrac{x-3}{x+5}$ trên khoảng $\left( -\infty ;-5 \right)$ và trên khoảng $\left( -5;+\infty \right)$. Khẳng định nào sau đây đúng?

Cho hàm số $f\left( x \right)=\sqrt{2x-7}.$ Khẳng định nào sau đây đúng?

Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $\left[ -3;3 \right]$ để hàm số $f\left( x \right)=\left( m+1 \right)x+m-2$ đồng biến trên $\mathbb{R}$?

Tất cả các giá trị thực của tham số $m$ để hàm số $y=-{{x}^{2}}+\left( m-1 \right)x+2$ nghịch biến trên khoảng $\left( 1;2 \right)$ là

Cho hàm số $y=f\left( x \right)$ có tập xác định là $\left[ -3;3 \right]$ và đồ thị như hình vẽ.

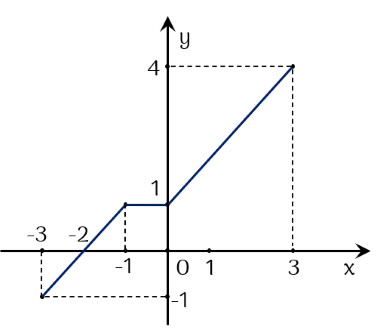
Khẳng định nào sau đây là đúng?

Cho đồ thị hàm số $y={{x}^{3}}$ như hình bên.

Khẳng định nào sau đây sai?

Khẳng định nào sau đây đúng với hàm số $y = |x|$?