Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tự luận (7 điểm) SVIP
(2 điểm)
1) Hoa đun nước và đo nhiệt độ của nước tại một số thời điểm sau khi bắt đầu đun được kết quả như sau:
| Số phút sau khi bắt đầu đun |
$4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
| Nhiệt độ $\left( ^{\circ} \mathrm{C}\right)$ | $42$ | $75$ | $83$ | $91$ | $98$ | $100$ | $105$ |
a) Hoa đã thu được dữ liệu trên bằng cách nào trong số các cách sau: quan sát, làm thí nghiệm hay lập bảng hỏi? (0,5 điểm)
b) Tìm các giá trị không hợp lí (nếu có) trong dữ liệu về nhiệt độ của nước mà Hoa đo được và giải thích? (0,5 điểm)
2) Cho dữ liệu ban đầu sau cho biết điểm kiểm tra môn Ngữ Văn của $10$ bạn trong tổ 1 lớp 6B.
$6$ ; $7$ ; $6$ ; $5$ ; $8$ ; $8$ ; $7$ ; $7$ ; $6$ ; $5$
a) Lập bảng thống kê theo mẫu dưới đây. (0,5 điểm)
| Điểm | $5$ | ... | ... | ... |
| Số bạn | $2$ | ... | ... | ... |
b) Hãy cho biết đối tượng thống kê và tiêu chí thống kê. (0,5 điểm)
Hướng dẫn giải:
1)
a) Hoa thu được dữ liệu trên bằng cách làm thí nghiệm (đo nhiệt độ nước tại một số thời điểm khi bắt đầu đun).
b) Giá trị $105$ là giá trị không hợp lí vì ở điều kiện bình thường, nước sôi ở $100$ độ C và sẽ bay hơi.
2)
a)
| Điểm | $5$ | $6$ | $7$ | $8$ |
| Số bạn | $2$ | $3$ | $3$ | $2$ |
b) Đối tượng thống kê: Điểm kiểm tra môn Ngữ văn.
Tiêu chí thống kê: Điểm kiểm tra môn Ngữ văn được thống kê theo từng bạn trong tổ 1.
(1,5 điểm)
1) Trong hộp có $1$ bóng xanh, $1$ bóng đỏ và $1$ bóng vàng. Hòa lấy ra ngẫu nhiên một quả bóng trong hộp, ghi màu quả bóng rồi trả nó lại hộp. Kết quả $9$ lần lấy bóng cho ở bảng sau:
| Lần thứ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Màu bóng | Xanh | Vàng | Xanh | Đỏ | Xanh | Xanh | Vàng | Đỏ | Vàng |
a) Hãy cho biết có bao nhiêu kết quả khác nhau có thể xảy ra trong mỗi lần lấy bóng. (0,5 điểm).
b) Nêu hai điều cần chú ý trong mô hình xác suất của trò chơi trên. (0,5 điểm).
c) Tính xác suất thực nghiệm của kết quả bạn Hòa lấy ra quả bóng màu Xanh. (0,5 điểm).
Hướng dẫn giải:
1)
a) Có $3$ kết quả khác nhau trong mỗi lần lấy bóng là:
- Hòa lấy ra quả bóng đỏ (kí hiệu: Đ).
- Hòa lấy ra quả bóng xanh (kí hiệu: X).
- Hòa lấy ra quả bóng vàng (kí hiệu: V).
b) Hai điều chú ý của mô hình xác suất là:
- Hòa lấy ra ngẫu nhiên một quả bóng trong hộp.
- Tập hợp các kết quả có thể xảy ra là: {Đ, X, V}. Các kí hiệu được giải thích ở phần trên.
c) Trong $9$ lần lấy ngẫu nhiên, có $4$ lần bạn Hòa lấy ra quả bóng màu Xanh.
Xác suất thực nghiệm của kết quả bạn Hòa lấy ra quả bóng màu Xanh là:
$4:9=\dfrac{4}{9}$
(3,5 điểm)
1) Quan sát hình dưới đây
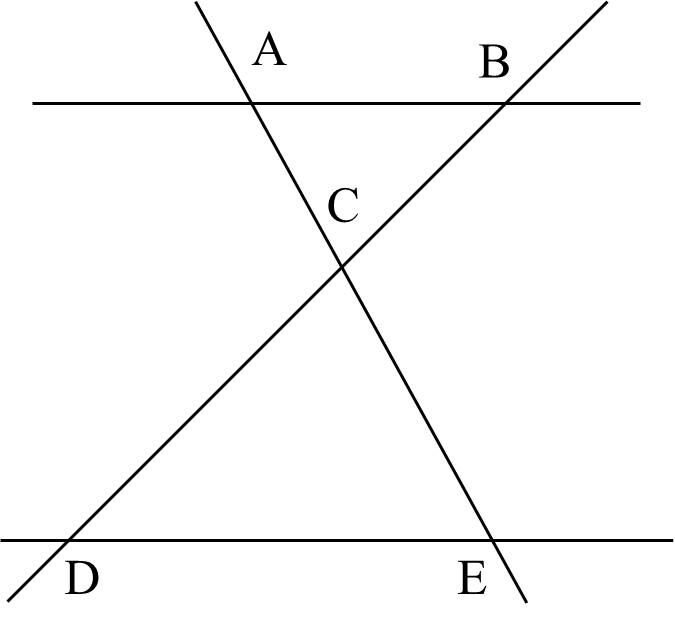
a) Chỉ ra các điểm thuộc đoạn thẳng $BD$, các điểm không thuộc đoạn thẳng $BD$. (0,25 điểm).
b) Chỉ ra các cặp đường thẳng song song. (0,25 điểm).
c) Chỉ ra các cặp đường thẳng cắt nhau và xác định giao điểm của chúng. (0,5 điểm).
2) Cho đoạn thẳng $ {MN}=8$ cm. Gọi $ {R}$ là trung điểm của $ {MN}$.
a) Tính $MR$; $RN$. (0,5 điểm)
b) Lấy hai điểm $P$ và $Q$ trên đoạn thẳng $M N$ sao cho $M P=NQ=3$ cm. Điểm $ {R}$ có là trung điểm của $PQ$ không? Vì sao? (1,5 điểm)
3) Cho trước $12$ điểm, trong đó có đúng $4$ điểm thẳng hàng. Vẽ các đường thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đường thẳng? (0,5 điểm)
Hướng dẫn giải:
1)
a) Tập hợp các điểm thuộc đoạn thẳng $BD$ là ${B;C;D}$, tập hợp các điểm thuộc không đoạn thẳng $BD$ là ${A;E}$.
b) Cặp đường thẳng song song là $AB$ // $DE$.
c) Gợi ý: Liệt kê theo các giao điểm, có 5 giao điểm nên có 5 cặp đường thẳng cắt nhau.
Các cặp đường thẳng cắt nhau là
$AB$ và $AE$ cắt nhau tại $A$.
$BA$ và $BD$ cắt nhau tại $B$.
$AE$ và $BD$ cắt nhau tại $C$.
$DE$ và $DB$ cắt nhau tại $D$.
$EA$ và $ED$ cắt nhau tại $E$.
2)
a)
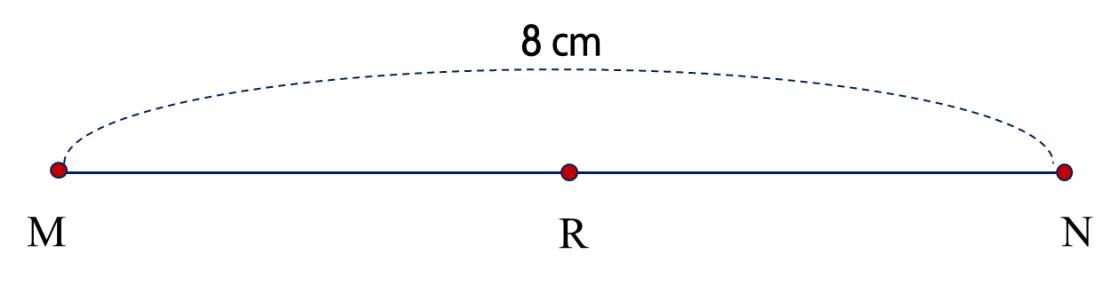
Vì $R$ là trung điểm của đoạn thẳng $MN$, nên ta có $MR=RN=MN:2$.
Độ dài của đoạn thẳng $MR$ hay $RN$ là:
$8:2=4$ (cm)
b)
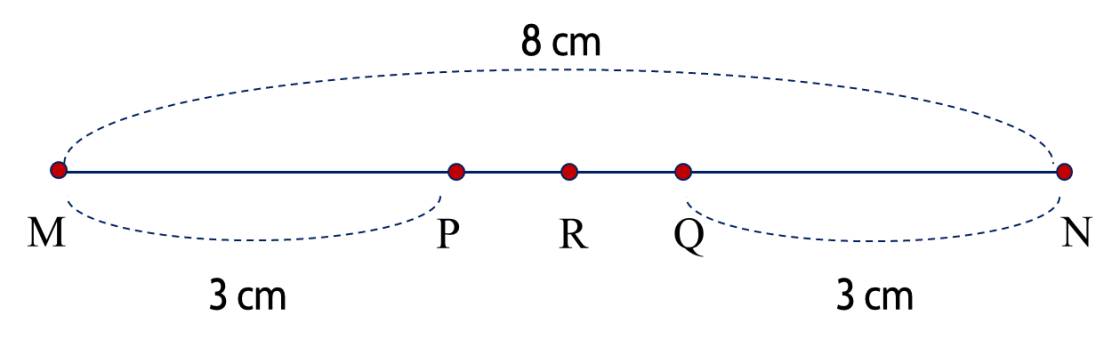
Nhìn hình vẽ, ta thấy $R$ nằm giữa $P$ và $Q$; $MN=MP+PQ+QN$; $MR=MP+PR$.
Độ dài của đoạn thẳng $PQ$ là
$8-3-3=2$ (cm).
Độ dài của đoạn thẳng $PR$ là
$4-3=1$ (cm).
Từ đây, ta thấy $PR:PQ=\dfrac{1}{2}$,
Vậy $R$ là trung điểm $PQ$.
3)
Chọn 1 điểm nối với $11$ điểm còn lại ta được $11$ đường thẳng, làm như thế với $12$ điểm ta được $12.(12-1)=132$ đường thẳng. Nhưng mỗi đường thẳng lặp lại $2$ lần nên số đường thẳng vẽ được là $132:2=66$ đường thẳng.
Qua $4$ điểm không thẳng hàng sẽ vẽ được $6$ đường thẳng.
Qua $4$ điểm thẳng hàng vẽ được $1$ đường thẳng nên số đường thẳng giảm đi $5$ đường thẳng
Vậy số đường thẳng vẽ được là $66-5=61$ đường thẳng vậy ta vẽ được 61 đường thẳng.
