Phần tự Luận (6 điểm) SVIP

Hướng dẫn giải:

a) 
$\begin{aligned}
& x^{2}-4 x-5=0 \\
\Leftrightarrow & x^{2}-5 x+x-5=0 \\
\Leftrightarrow & x(x-5)+(x-5)=0 \\
\Leftrightarrow &(x-5)(x+1)=0 \\
\Leftrightarrow & {\left[\begin{array} { l } 
{ x - 5 = 0 } \\
{ x + 1 = 0 }
\end{array} \Leftrightarrow \left[\begin{array}{l}
x=5 \\
x=-1
\end{array}\right.\right.}
\end{aligned}$
Vậy phương trình có tập nghiệm là $S=\{-1 ; 5\}$.

b) Điều kiện: $x \geq 0, x \neq 4$.
$A=\dfrac{x+2 \sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}$ $=\dfrac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-2)(\sqrt{x}+2)}$ $=\dfrac{\sqrt{x}}{\sqrt{x}-2} .$

Vậy $A=\dfrac{\sqrt{x}}{\sqrt{x}-2}$ khi $x \geq 0, x \neq 4$.

Hướng dẫn giải:

Gọi giá niêm yết của quạt điện là $x$ (dồng) $\left(x \in N^{*}, x<900000\right)$
Giá niêm yết của chiếc đèn tích điện là $y$ (đồng) $\left(y \in \mathbb{N}^{*}, y<900000\right)$
$\Rightarrow$ Giá của quạt điện sau khi giảm $15\%$ là $x-0,15 x=0,85 x$ (đổng)
Giá của chiếc đèn tích điện sau khi giảm $10 \%$ là $y-0,1 y=0,9 y$ (đồng)
Do tổng số tiền theo giá niêm yết của hai sản phẩm là 900000 đồng và tổng số tiền sau khi đã giảm giá của đồng nên ta có hề phương trinh:
$\left\{\begin{array}{l}
x+y=900000 \\
0,85 x+0,9 y=780000
\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}
y=900000-x \\
0,85 x+0,9,(900000-x)=780000
\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}
y=900000-x \\
0,85 x+810000-0,9 x=780000
\end{array}\right.$
$\Leftrightarrow\left\{\begin{array} { l } 
{ 0 , 0 5 x = 3 0 0 0 0 } \\
{ y = 9 0 0 0 0 0 - x }
\end{array}\right.$

$\Leftrightarrow \left\{\begin{array}{l}
x=600000 \\
y=300000
\end{array}(tm)\right.$
Vậy giá niêm yết của quạt điện là 600000 đồng và giá niêm yết của chiếc đèn tích điện là 300000 đồng.

Hướng dẫn giải:

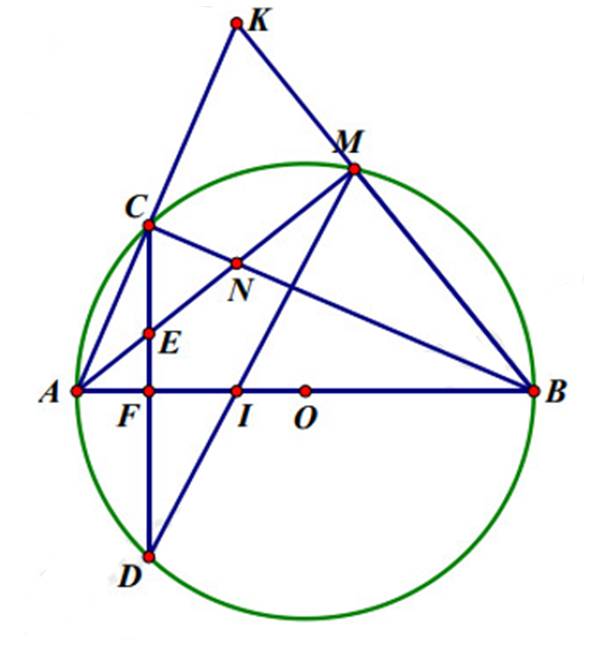
a) Chứng minh tứ giác EFBM nội tiếp được trong một đường tròn và $\widehat{ C M A}=\widehat{ D M A}$
Vì $M \in(O) ; A B$ là đường kính của $(O)$
$\Rightarrow \widehat{ A M B}=90^{\circ}$
Ta có: $C D \perp A B$ tại $F$ (gt), $E \in C D \Rightarrow \widehat{ E F B}=90^{\circ}$
Xét tứ giác $E F B M$, có:
$\widehat{ A M B}=90^{\circ}$
$\widehat{ E F B}=90^{\circ}$
Mà hai góc này ở vị trí đối nhau
$\Rightarrow$ Tứ giác $E F B M$ nội tiếp một đường tròn (đpcm).
Vì $C D \perp A B$ tại $F$ (gt) $\Rightarrow F$ là trung điểm của $C D$ (định lí về mối liên hệ giữa đường kính và dây cung) Xét $\triangle A C D$ có:
$F$ là trung điểm của $C D(\mathrm{cmt})$
$A F \perp C D$ (do $A B \perp C D, F \in A B)$ )
$\Rightarrow A F$ là đường cao đồng thời là đường trung trực của $\triangle A C D$
$\Rightarrow \triangle A C D$ cân tại $A$
$\Rightarrow \widehat{ A C D}=\widehat{ A D C}$ (tính chất)
Mà $\widehat{ A D C}=\widehat{ C M A}$ (2 góc nội tiếp cùng chắn cung $A C$ )
$\widehat{ A M D}=\widehat{ A C D}$ (2 góc nội tiếp cùng chắn cung $A D$ )
Do đó: $\widehat{ A M D}=\widehat{ C M A}(đ p c m)$
b) Gọi giao điểm của hai đường thẳng $A C$ và $B M$ là $K$; giao điểm của hai đurờng thẳng $D M$ và $A B$ là I; giao điểm của hai đường thẳng $A M$ và $B C$ là $N$. Chứng minh ba điểm $K, N, I$ thẳng hàng.
Ta có: $\widehat{ A C B}=90^{\circ}$ ( góc nội tiếp chắn nửa đường tròn) $\Rightarrow C B \perp A C$ hay $C B \perp A K$
$\widehat{ A M B}=90^{\circ}$ ( góc nội tiếp chắn nửa đường tròn) $\Rightarrow A M \perp M B$ hay $A M \perp B K$
Xét $\triangle A K B$ có:
$C B \perp A K$
Mà $C B \cap A N=\{N\}$
$\Rightarrow N$ là trực tâm của $\triangle A K B$
$\Rightarrow K N$ là đường cao thứ ba của $\triangle A K B$
$\Rightarrow K N \perp A B$ (1)
Ta có: $\widehat{ N M I}=\widehat{ I B N}$ (cùng bằng với góc $\widehat{ A D C}$ )
Xét tứ giác $N M B I$ có: $\widehat{ N M I}=\widehat{ I B N}(\mathrm{cmt})$
Mà hai góc này cùng nhìn cạnh $I N$ dưới một góc không đổi.
$\Rightarrow$ Tứ giác $N M B I$ nội tiếp một đường tròn
$\Rightarrow \widehat{ N M B}+\widehat{ N I B}=180^{\circ}$ (2 góc đối nhau)
$\Rightarrow 90^{\circ}+\widehat{ N I B}=180^{\circ}$
$\Rightarrow \widehat{ N I B}=90^{\circ}$
$\Rightarrow N I \perp I B$ tại $I$ hay $N I \perp A B$ tại $I$ (2)
(1),(2) $\Rightarrow K, N, I$ thằng hàng (đpcm).

Hướng dẫn giải:

Ta có:
$
\begin{aligned}
&P=\dfrac{3(b+c)}{2 a}+\dfrac{4 a+3 c}{3 b}+\dfrac{12(b-c)}{2 a+3 c} \\
&=\left[\dfrac{3(b+c)}{2 a}+2\right]+\left[\dfrac{4 a+3 c}{3 b}+1\right]+\left[\dfrac{12(b-c)}{2 a+3 c}+8\right]-11 \\
&=\dfrac{4 a+3 b+3 c}{2 a}+\dfrac{4 a+3 b+3 c}{3 b}+\dfrac{4(4 a+3 b+3 c)}{2 a+3 c}-11 \\
&=(4 a+3 b+3 c)\left(\dfrac{1}{2 a}+\dfrac{1}{3 b}+\dfrac{4}{2 a+3 c}\right)-11 \\
&=[2 a+3 b+(2 a+3 c)]\left(\dfrac{1}{2 a}+\dfrac{1}{3 b}+\dfrac{4}{2 a+3 c}\right)-11 \\
&\geq(1+1+2)^{2}-11=5.
\end{aligned}
$
Dấu bằng xảy ra $\Leftrightarrow 2 a=3 b=\dfrac{2 a+3 c}{2}$
$
\Leftrightarrow\left\{\begin{array} { l } 
{ 2 a = 3 b } \\
{ 4 a = 2 a + 3 c }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
2 a=3 b \\
2 a=3 c
\end{array} \Leftrightarrow 2 a=3 b=3 c\right.\right.
$
Vậy giá trị nhỏ nhất của $P=5$ khi $2 a=3 b=3 c$.