Vị trí tương đối của hai đường tròn SVIP

Hướng dẫn giải:

Trường hợp 1: (O) và (O’) tiếp xúc trong.

Xét $\Delta OAC$, ta có:

$\frac{O^\prime B}{OC}=\frac{r}{R}=\frac{O^\prime A}{OA}\Rightarrow O^\prime B$ // $OC$.

Suy ra các tiếp tuyến tại B và C song song với nhau vì chúng lần lượt vuông góc với O’B và OC.

Trường hợp 2: (O) và (O’) tiếp xúc ngoài.

Ta thấy $\Delta O^\prime AB\backsim\Delta OAC$ (g.g) $\Rightarrow\frac{O^\prime B}{OC}=\frac{r}{R}=\frac{O^\prime A}{OA}$

$\Rightarrow O^\prime B$ // $OC$.

Lập luận tương tự như trên, ta được điều phải chứng minh.

Hướng dẫn giải:

Gọi các tiếp điểm của các tiếp tuyến chung trong là E, F, G, H như hình.

Theo tính chất hai tiếp tuyến cắt nhau: DE = DA, DF = CB, CA = CG và DH = DB.

Do đó: DE + DB = AB = CF + CA = 2AC + GF = 2BD + HE, do GF = HE nên AC = BD.

Hướng dẫn giải:

a. Tam giác DBE có đường trung tuyến BO bằng $\frac{1}{2}$ ED nên là tam giác vuông, suy ra $\widehat{DBE}={90}^\circ$

$\Rightarrow \widehat{OBE}=\widehat{DBA}$ (vì cùng phụ với $\widehat{DBO}$) (1)

Trong tam giác cân OBE, ta có $\widehat{OBE}=\widehat{OEB}$ (2)

Từ (1) và (2) ta được $\widehat{OEB}=\widehat{DBA}$.

Suy ra $\Delta ADB\ \backsim\Delta ABE$ (g.g) (Vì chúng có chung góc A).

Ta được $d\frac{AD}{AB}=\dfrac{AB}{AE}\Rightarrow AD.AE=AB^2$.

b. Từ kết quả câu a, ta có

$\frac{DE}{AE}=\frac{AD}{DE}\Rightarrow\frac{DE}{AE-DE}=\frac{AD}{DE-AD}$.

Lại có: DE = 2BO = AB (giả thiết) và AD = AC nên:

$\frac{AD}{AB}=\frac{AD}{AB-AC}\Rightarrow\frac{AB}{AC}=\frac{AC}{CB}\Rightarrow AC^2=CB.AB$.

c. $\Delta DAM\backsim\Delta DON$ (g.g) $\Rightarrow\frac{DM}{DN}=\frac{AD}{OD}$.

Tương tự, $\frac{DP}{DB}=\frac{AD}{OD}\Rightarrow\Delta DPM\backsim\Delta DBN$ (c.g.c).

Hướng dẫn giải:

Kẻ  \(OH\perp CA,\) \(O'K\perp AD\) (H, K thuộc CD). Suy ra OH//O'K.
Vì vậy tứ giác HOO'K là hình thang có I là trung điểm của OO'.
Mà IA//OH//O'K (cùng vuông góc với CD).
Suy ra A là trung điểm của HK hay AH = AK.

Lại có do \(OH\perp CA,\) \(O'K\perp AD\) nên H và K lần lượt là trung điểm của AC và AD (đường kính - dây cung).
Suy ra AD = AC.

Hướng dẫn giải:

Gọi I là trung điểm của OO'.
Có OB//O'C (cùng vuông góc vuông góc vói BC).
Suy ra tứ giác OBCO' là hình thang.
Có I và M lần lượt là trung điểm của OO' và BC nên IM là đường trung bình của hình thang vuông OBCO'.
Suy ra: \(IM\perp BC\) ; \(IM=\dfrac{OB+OC}{2}=\dfrac{OO'}{2}\).

Vì vậy BC là tiếp tuyến của đường tròn đường kính OO' tại M.

Hướng dẫn giải:

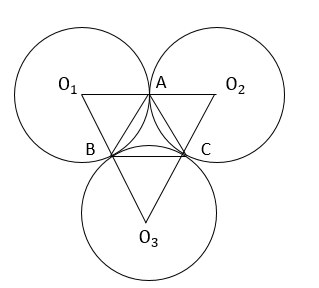
Gọi A, B, C lần lượt là ba tiếp điểm của ba đường tròn.
Tam giác \(O_1O_2O_3\) đều có \(O_1A=AO_2\) nên A là trung điểm của \(O_1O_2\).
Tương tự B, C lần lượt là trung điểm của \(O_2O_3,O_3O_1\).
Suy ra: AB = BC = AC = r.

Thế nên ABC là tam giác đều cạnh r.
Vậy diện tích tam giác ABC là: \(\dfrac{1}{2}AB.AC.\sin\widehat{BAC}=\dfrac{1}{2}a.a.\sin60^o=\dfrac{\sqrt{3}}{4}a^2\).

Hướng dẫn giải:

Nối OO', OB, OC.
Các tam giác OBA và O'AC cân tại O và O'.
Do \(\widehat{BAO}=\widehat{O'AC}\) nên \(\widehat{OBA}=\widehat{O'CA}\) .
Mặt khác do $xy$//$uv$ nên \(\widehat{yBA}=\widehat{ACu}\).
Suy ra \(\widehat{O'Cu}=\widehat{O'CA}+\widehat{ACu}=\widehat{OBA}+\widehat{yBA}=90^o\).
Suy ra \(O'C\perp uv\) hay $uv$ là tiếp tuyến của đường tròn (O').

Hướng dẫn giải:

a) Trong tam giác OIK có:

|OK \(-\) OI| < IK < |OK + OI| hay \(\left|R-r\right|< IK< \left|R+r\right|\).

Vậy hai đường tròn (I) và (K) luôn cắt nhau.
b) Dễ thấy tứ giác OMCN là hình chữ nhật (Tứ giác có 3 góc vuông). 
Mà OM = OI + IM = OI + OK;

      ON = OK + KN = OK + OI.
Vậy OM = ON hay hình chữ nhật OMCN là hình vuông.
c) Gọi giao điểm của BK và MC là L và giao điểm của AB với MC là P.
Tứ giác IBKO là hình chữ nhật. Suy ra IB = OK.
Tứ giác MLBI là hình vuông nên ML = BI, BL = OK.
Từ đó suy ra \(\Delta BLP=\Delta KOI\).  Vì vậy LP = OI.
Suy ra MP = ON = MC. Hay điểm C trùng với P.
Suy ra ba điểm A, B, C thẳng hàng.
d) Nếu OI + OK = a (không đổi) thì OM = MC = a không đổi. Suy ra điểm C cố định.
Vậy đường thẳng AB luôn đi qua điểm C cố định.