\(M=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...-\frac{1}{2018}+\frac{1}{2019}\)

\(M=\left(1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{2019}\right)-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+...+\frac{1}{2018}\right)\)

\(M=\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2018}+\frac{1}{2019}\right)-2\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+...+\frac{1}{2018}\right)\)

\(M=\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2019}\right)-\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{1009}\right)\)

\(M=\frac{1}{1010}+\frac{1}{1011}+...+\frac{1}{2019}=N\)

Suy ra \(\left(M-N\right)^2=0\).

\(\left(\frac{1}{a};\frac{1}{b};c\right)=\left(x;y;z\right)\)\(\Rightarrow\)\(x+y+z\le2\)

\(P=\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}+x+y+z=\Sigma\left(\frac{1}{x^2}+\frac{27}{8}x+\frac{27}{8}x\right)-\frac{23}{4}\left(x+y+z\right)\ge\frac{35}{4}\)

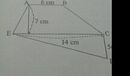
Diện tích hình thang \(ABCE\)là: 

\(\left(14+6\right)\div2\times7=70\left(cm^2\right)\)

Diện tích tam giác \(DCE\)là: 

\(5\times14\div2=35\left(cm^2\right)\)

Diện tích \(ABCDE\)là: 

\(70+35=105\left(cm^2\right)\)

Dịch dấu phẩy sang phải một hàng thì số mới hơn 10 lần số cũ.

   Ta có sơ đồ:

    Số cũ: -----

                                                 Hiệu: 47,34

    Số mới: ----- ----- ----- ----- ----- ----- ----- ----- ----- -----

    Số phải tìm là: 47,34:[10-1]=5,26

                                Đ/S:5,26

Dạng bài tổng tỉ nha

a/ Ta có

\(AB\perp AC;CE\perp AC\) => AB//CE \(\Rightarrow\widehat{ABD}=\widehat{BEC}\) (Góc so le trong) (1)

\(\widehat{ABD}=\widehat{EBC}\) (Đề bài) (2)

Từ (1) và (2) \(\Rightarrow\widehat{BEC}=\widehat{EBC}\) => tam giác BCE cân tại C

b/ Do tam giác BCE cân tại C => CE=BC

Mà trong tam giác vuông ABC có BC>AB (trong tg vuông cạnh huyền là cạnh lớn nhất) => CE>AB

mình k có bạn

Ta có: dài hcn 100% ; rộng hcn 100%

CD sau khi tăng: 100%+10%=110% 

CR sau khi giảm: 100%-10%=90%

S hcn ban đầu: 100% x 99%=99%

Vì 99%<100% nên S hcn giảm đi 1%

     ĐS: 1%

Cái kia sai nhá bạn

Gọi số đo chiều dài là 100 x a

                 Số đo chiều rộng là 100 x b

          Số đo diện tích là : 10 000 x a x b

          Số đo chiều dài mới là : 110 x a

         số đo chiều rộng mới là :  90 x b

          Số đo diện tích  mới là : 9900 x a x b

          Số đo diện tích mới kém số đo diện tích cũ là :

                   10 000 x a x b – 9 900 x a x b = 100 x a x b

            Tức là kém diện tích cũ là :   100 × a × b 1000 × a × b =10%

                                                                            Bài giải 

                                           1/5 của 45 bông là số bông hoa là :

                                                 45 :5 x1 = 9 ( bông )

                                                                        Đ/S : 9 bông hoa .

ko cần x 1 cũng đc nha em 

chúc em hok tốt #

\(\frac{1}{5}\)của \(45\)bông hoa là: \(\frac{1}{5}\cdot45=9\)(bông hoa)

a) Ta có: \(1-\frac{9}{10}=\frac{1}{10}\)

\(1-\frac{10}{11}=\frac{1}{11}\)

Vì \(\frac{1}{10}>\frac{1}{11}\Rightarrow1-\frac{9}{10}>1-\frac{10}{11}\Rightarrow\frac{9}{10}< \frac{10}{11}\)

b) \(1-\frac{125}{251}=\frac{126}{251}\)

\(1-\frac{127}{253}=\frac{126}{253}\)

Vì \(\frac{126}{251}>\frac{126}{253}\Rightarrow1-\frac{125}{251}>1-\frac{127}{253}\Rightarrow\frac{125}{251}< \frac{127}{253}\)

tự làm đi cho có ý thức đi nhé