a: Xét ΔEHB vuông tại E và ΔDHC vuông tại D có

\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)

Do đó: ΔEHB~ΔDHC

b: Xét ΔABC có

BD,CE là các đường cao

DB cắt CE tại H

Do đó: H là trực tâm của ΔABC

=>AH\(\perp\)BC tại F

Xét ΔBFH vuông tại Fvà ΔBDC vuông tại D có

\(\widehat{FBH}\) chung

Do đó: ΔBFH~ΔBDC

=>\(\dfrac{BF}{BD}=\dfrac{BH}{BC}\)

=>\(BF\cdot BC=BH\cdot BD\)

c: Xét ΔCFH vuông tại F và ΔCEB vuông tại E có

\(\widehat{FCH}\) chung

Do đó: ΔCFH~ΔCEB

=>\(\dfrac{CF}{CE}=\dfrac{CH}{CB}\)

=>\(CF\cdot CB=CH\cdot CE\)

\(BH\cdot BD+CH\cdot CE\)

\(=BF\cdot BC+CF\cdot BC=BC\left(BF+CF\right)=BC^2\)

a: ΔABC vuông tại B

=>\(AB^2+BC^2=AC^2\)

=>\(AC=\sqrt{12^2+9^2}=15\left(cm\right)\)

b: Xét ΔHBA vuông tại H và ΔHCB vuông tại H có

\(\widehat{HBA}=\widehat{HCB}\left(=90^0-\widehat{HAB}\right)\)

Do đó: ΔHBA~ΔHCB

=>\(\dfrac{HB}{HC}=\dfrac{HA}{HB}\)

=>\(HB^2=HA\cdot HC\)

c: Đề sai rồi bạn

Đề không đủ dữ kiện để tính toán. Bạn xem lại nhé. 

Chọn D

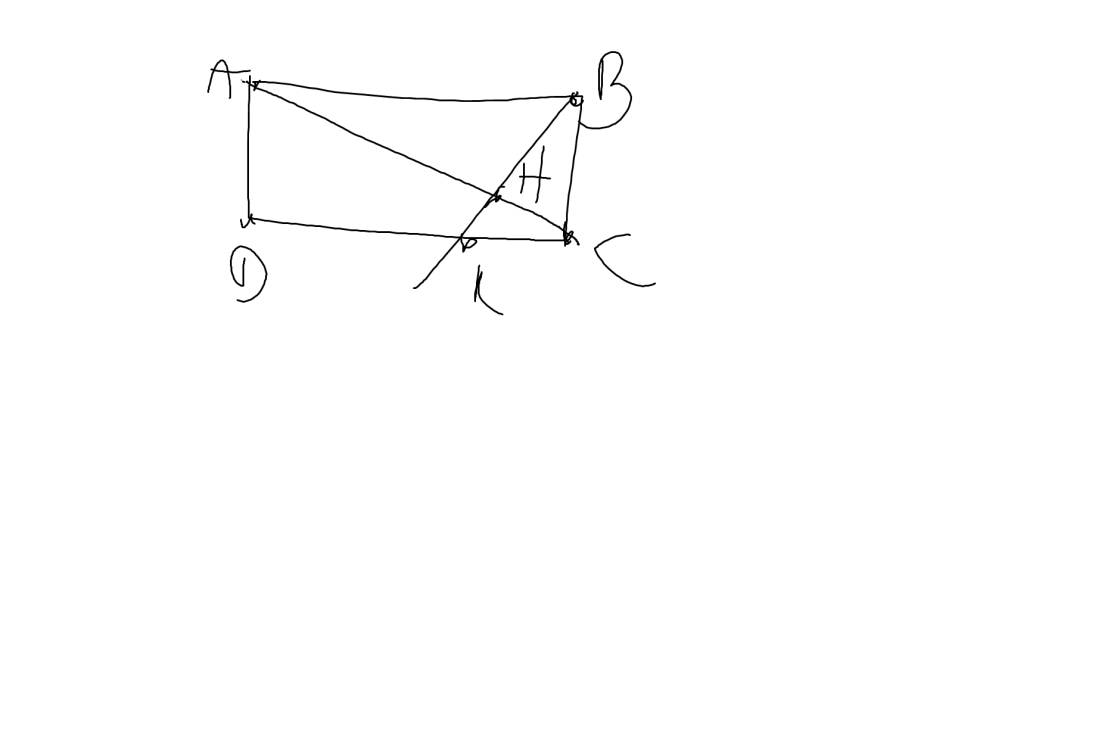
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

\(\widehat{ABC}\) chung

Do đó: ΔABC~ΔHBA

b: Ta có: \(\widehat{HAD}+\widehat{BDA}=90^0\)(ΔHAD vuông tại H)

\(\widehat{CAD}+\widehat{BAD}=\widehat{BAC}=90^0\)

mà \(\widehat{BDA}=\widehat{BAD}\)(ΔBAD cân tại B)

nên \(\widehat{HAD}=\widehat{CAD}\)

=>AD là phân giác của góc HAC

Xét ΔAHC có AD là phân giác

nên \(\dfrac{DH}{DC}=\dfrac{AH}{AC}\)

=>\(DH\cdot AC=AH\cdot DC\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔHBA~ΔABC

b: Xét ΔBAM vuông tại A và ΔBHN vuông tại H có

\(\widehat{ABM}=\widehat{HBN}\)

Do đó: ΔBAM~ΔBHN

=>\(\dfrac{AB}{HB}=\dfrac{AM}{HN}\)

=>\(AB\cdot HN=AM\cdot HB\)

ĐKXĐ: x<>-2

\(x^2+\dfrac{4x^2}{\left(x+2\right)^2}=5\)

=>\(\dfrac{\left(x^2+2x\right)^2+4x^2}{\left(x+2\right)^2}=5\)

=>\(x^4+4x^3+4x^2+4x^2=5\left(x^2+4x+4\right)\)

=>\(x^4+4x^3+8x^2-5x^2-20x-20=0\)

=>\(x^4+4x^3+3x^2-20x-20=0\)

=>\(\left(x-2\right)\left(x+1\right)\left(x^2+5x+10\right)=0\)

mà \(x^2+5x+10>0\forall x\)

nên (x-2)(x+1)=0

=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)

a: Xét ΔABC vuông tại A và ΔMBE vuông tại M có

\(\widehat{ABC}\) chung

Do đó: ΔABC~ΔMBE

b: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{18^2+24^2}=30\left(cm\right)\)

M là trung điểm của BC

=>\(MB=MC=\dfrac{BC}{2}=15\left(cm\right)\)

ΔBAC~ΔBME

=>\(\dfrac{BA}{BM}=\dfrac{BC}{BE}=\dfrac{AC}{ME}\)

=>\(\dfrac{18}{15}=\dfrac{30}{BE}=\dfrac{24}{ME}\)

=>\(\dfrac{30}{BE}=\dfrac{24}{ME}=\dfrac{6}{5}\)

=>BE=25(cm); ME=20(cm)

c: Xét ΔHMC vuông tại M và ΔHAE vuông tại A có

\(\widehat{MHC}=\widehat{AHE}\)(hai góc đối đỉnh)

Do đó: ΔHMC~ΔHAE

=>\(\dfrac{HM}{HA}=\dfrac{HC}{HE}\)

=>\(HM\cdot HE=HC\cdot HA\)

d: Xét ΔCEB có

CA,EM là các đường cao

CA cắt EM tại H

Do đó: H là trực tâm của ΔCEB

=>BH\(\perp\)CE tại N

Xét ΔCNB vuông tại N và ΔCME vuông tại M có

\(\widehat{NCB}\) chung

Do đó: ΔCNB~ΔCME

=>\(\dfrac{CN}{CM}=\dfrac{CB}{CE}\)

=>\(\dfrac{CN}{CB}=\dfrac{CM}{CE}\)

Xét ΔCNM và ΔCBE có

\(\dfrac{CN}{CB}=\dfrac{CM}{CE}\)

\(\widehat{NCM}\) chung

Do đó: ΔCNM~ΔCBE

=>\(\widehat{CMN}=\widehat{CEB}\)

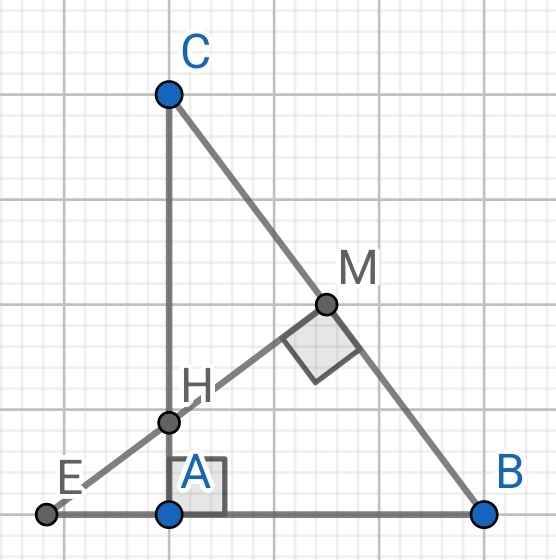
a) Sửa đề: Chứng minh ∆ABC ∽ ∆MBE

Xét hai tam giác vuông: ∆ABC và ∆MBE có:

∠B chung

⇒ ∆ABC ∽ ∆MBE (g-g)

b) ∆ABC vuông tại A (gt)

⇒ BC² = AB² + AC² (Pythagore)

= 18² + 24²

= 900

⇒ BC = 30 (cm)

Do M là trung điểm của BC (gt)

⇒ BE = BC : 2 = 30 : 2 = 15 (cm)

Do ∆ABC ∽ ∆MBE (cmt)

⇒ AB/MB = AC/EM

⇒ 18/15 = 24/EM

⇒ EM = 15 . 24 : 18 = 20 (cm)

c) Xét hai tam giác vuông: ∆HMC và ∆HAE có:

∠MHC = ∠AHE (đối đỉnh)

⇒ ∆HMC ∽ ∆HAE (g-g)

⇒ HM/HA = HC/HE

⇒ HM.HE = HA.HC

Ko em nhé

Theo mình thì hạnh kiểm HK 2 sẽ là khá nha