Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
c: \(P=A:B=\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}:\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)
\(=\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{\sqrt{x}-1}=\dfrac{2\sqrt{x}+3}{\sqrt{x}-1}\)
Để P là số nguyên thì \(2\sqrt{x}+3⋮\sqrt{x}-1\)
=>\(2\sqrt{x}-2+5⋮\sqrt{x}-1\)
=>\(5⋮\sqrt{x}-1\)
=>\(\sqrt{x}-1\in\left\{1;-1;5;-5\right\}\)
=>\(\sqrt{x}\in\left\{2;0;6;-4\right\}\)
=>\(\sqrt{x}\in\left\{2;0;6\right\}\)
=>\(x\in\left\{4;0;36\right\}\)
mà x lớn nhất
nên x=36
a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>PA\(\perp\)BD tại A
Xét (O) có
ΔCIB nội tiếp
CB là đường kính
Do đó: ΔCIB vuông tại I
Xét tứ giác ADHC có \(\widehat{DAC}+\widehat{DHC}=90^0+90^0=180^0\)
nên ADHC là tứ giác nội tiếp
b: Xét ΔDBP có
PA,BH là các đường cao
PA cắt BH tại C
Do đó: C là trực tâm của ΔDBP
=>DC\(\perp\)BP
mà CI\(\perp\)BP
mà DC,CI có điểm chung là C
nên D,C,I thẳng hàng
| GT | (O) có đường kính BC \(A\in\left(O\right);AP>AC;P\in AC\) PB\(\cap\)(O)={I} PH\(\perp\)BC tại H, PH cắt BA tại D |
| KL | a: ACHD nội tiếp b: D,C,I thẳng hàng |
a: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{CNM}\) là góc nội tiếp chắn cung CM
\(\widehat{CBM}\) là góc nội tiếp chắn cung CM
Do đó: \(\widehat{CNM}=\widehat{CBM}\)
mà \(\widehat{CBM}=\widehat{CED}\)(BEDC nội tiếp)
nên \(\widehat{HED}=\widehat{HNM}\)
=>ED//MN
c: Kẻ Ax là tiếp tuyến của (O) tại A
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{ADE}\left(=180^0-\widehat{EDC}\right)\)
nên \(\widehat{xAC}=\widehat{ADE}\)
=>Ax//DE
=>OA\(\perp\)DE
a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp
b: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB~ΔAFC
=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
=>\(AE\cdot AC=AF\cdot AB\)
c: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp đường tròn tâm I, đường kính BC
=>IE\(\perp\)EM tại E
Xét ΔABC có
BE,CF là các đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại K
Ta có: ΔIEB cân tại I
=>\(\widehat{IEB}=\widehat{IBE}\)
\(\widehat{MEI}=\widehat{MEH}+\widehat{IEH}=90^0\)
\(\widehat{BHK}+\widehat{HBK}=90^0\)
mà \(\widehat{IEH}=\widehat{IBE}\)
nên \(\widehat{MEH}=\widehat{BHK}\)
=>\(\widehat{MEH}=\widehat{MHE}\)
=>ME=MH
Ta có: \(\widehat{MEH}+\widehat{MEA}=\widehat{AEH}=90^0\)
\(\widehat{MHE}+\widehat{MAE}=90^0\)
mà \(\widehat{MEH}=\widehat{MHE}\)
nên \(\widehat{MEA}=\widehat{MAE}\)
=>MA=ME
=>MA=MH
=>M là trung điểm của AH
a: Sửa đề: Trên cung nhỏ BC lấy điểm E
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
Xét tứ giác BEFI có \(\widehat{BEF}+\widehat{BIF}=90^0+90^0=180^0\)
nên BEFI là tứ giác nội tiếp
b: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)DB tại C
Xét ΔAIF vuông tại I và ΔAEB vuông tại E có
\(\widehat{EAB}\) chung
Do đó: ΔAIF~ΔAEB
=>\(\dfrac{AI}{AE}=\dfrac{AF}{AB}\)
=>\(AI\cdot AB=AF\cdot AE\left(1\right)\)
Xét ΔACB vuông tại C có CI là đường cao
nên \(AI\cdot AB=AC^2\left(2\right)\)
Xét ΔADB vuông tại A có AC là đường cao
nên \(CA^2=CD\cdot CB\left(3\right)\)
Từ (1),(2),(3) suy ra \(AE\cdot AF=CB\cdot DC\)
Điều kiện:
\(\left\{{}\begin{matrix}x+\dfrac{3}{x}=\dfrac{x^2+3}{x}\ge0\\\dfrac{x^2+7}{2\left(x+1\right)}\ge0\end{matrix}\right.\)
mà \(x^2\ge0\forall x\Rightarrow\left\{{}\begin{matrix}x^2+3>0\forall x\\x^2+7>0\forall x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x^2+3}{x}\ge0\\\dfrac{x^2+7}{2\left(x+1\right)}\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>0\\2\left(x+1\right)>0\Leftrightarrow x+1>0\Leftrightarrow x>-1\end{matrix}\right.\)
\(\Leftrightarrow x>0\)
\(\sqrt{x+\dfrac{3}{x}}=\dfrac{x^2+7}{2\left(x+1\right)}\)
\(\Leftrightarrow\sqrt{\dfrac{x^2+3}{x}}=\dfrac{x^2+7}{2\left(x+1\right)}\)
\(\Leftrightarrow\left(\sqrt{\dfrac{x^2+3}{x}}\right)^2=\left[\dfrac{x^2+7}{2\left(x+1\right)}\right]^2\)
\(\Leftrightarrow\dfrac{x^2+3}{x}=\dfrac{\left(x^2+7\right)^2}{\left[2\left(x+1\right)\right]^2}\)
\(\Leftrightarrow\dfrac{x^2+3}{x}=\dfrac{x^4+14x^2+49}{4\left(x+1\right)^2}=\dfrac{x^4+14x^2+49}{4\left(x^2+2x+1\right)}=\dfrac{x^4+14x^2+49}{4x^2+8x+4}\)
\(\Leftrightarrow\dfrac{\left(x^2+3\right)\left(4x^2+8x+4\right)}{x\left(4x^2+8x+4\right)}=\dfrac{x\left(x^4+14x^2+49\right)}{x\left(4x^2+8x+4\right)}\)
\(\Leftrightarrow\left(x^2+3\right)\left(4x^2+8x+4\right)=x\left(x^4+14x^2+49\right)\)
\(\Leftrightarrow x^2\left(4x^2+8x+4\right)+3\left(4x^2+8x+4\right)=x\left(x^4+14x^2+49\right)\)
\(\Leftrightarrow4x^4+8x^3+4x^2+12x^2+24x+12=x^5+14x^3+49x\)
\(\Leftrightarrow4x^4+8x^3+16x^2+24x+12=x^5+14x^3+49x\)
\(\Leftrightarrow x^5-4x^4+14x^3-8x^3-16x^2+49x-24x-12=0\)
\(\Leftrightarrow x^5-4x^4+6x^3-16x^2+25x-12=0\)
\(\Leftrightarrow x^5-x^4-3x^4+3x^3+3x^3-3x^2-13x^2+13x+12x-12=0\)
\(\Leftrightarrow x^4\left(x-1\right)-3x^3\left(x-1\right)+3x^2\left(x-1\right)-13x\left(x-1\right)+12\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^4-3x^3+3x^2-13x+12\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^4-x^3-2x^3+2x^2+x^2-x-12x+12\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[x^3\left(x-1\right)-2x^2\left(x-1\right)+x\left(x-1\right)-12\left(x-1\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-1\right)\left(x^3-2x^2+x-12\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x^3-2x^2+x-12\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x^3-3x^2+x^2-3x+4x-12\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2\left[x^2\left(x-3\right)+x\left(x-3\right)+4\left(x-3\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x-3\right)\left(x^2+x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\\x^2+x+4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=3\left(tm\right)\\x^2+x+\dfrac{1}{4}+\dfrac{15}{4}=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=3\left(tm\right)\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{15}{4}=0\end{matrix}\right.\)
Có: \(\left(x+\dfrac{1}{2}\right)^2\ge0\forall x\Rightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{15}{4}>0\forall x\)
\(\Rightarrow x^2+x+4=0\) vô nghiệm
Vậy: \(x\in\left\{1;3\right\}\)
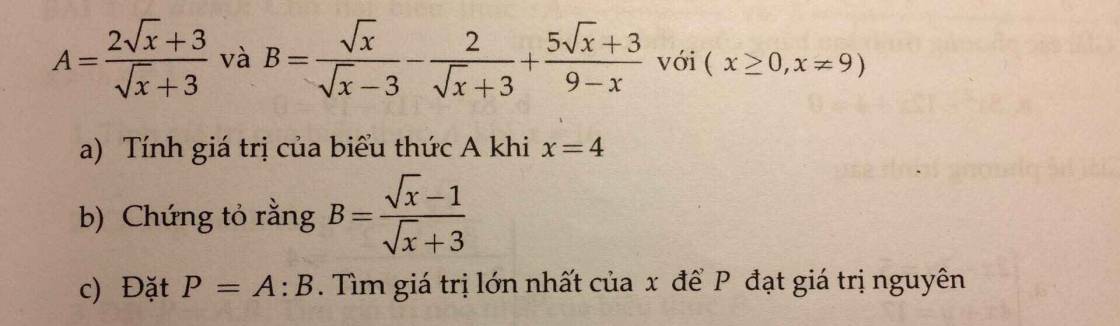
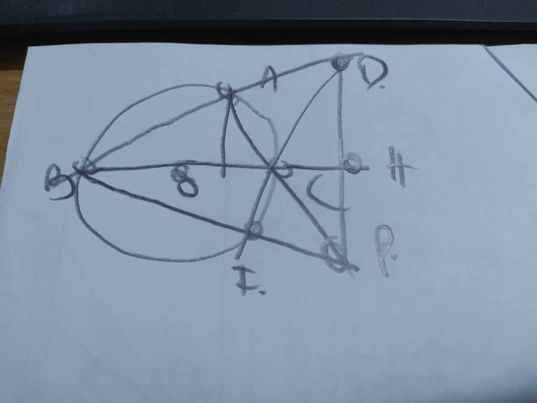
a: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
b: Ta có: BEDC là tứ giác nội tiếp
=>\(\widehat{BED}+\widehat{BCD}=180^0\)
mà \(\widehat{BED}+\widehat{AED}=180^0\)(hai góc kề bù)
nên \(\widehat{AED}=\widehat{ACB}\)
Xét ΔAED và ΔACB có
\(\widehat{AED}=\widehat{ACB}\)
\(\widehat{EAD}\) chung
Do đó: ΔAED~ΔACB