Mọi người giải giúp mình câu này với ạ, mình cảm ơn nhiều!
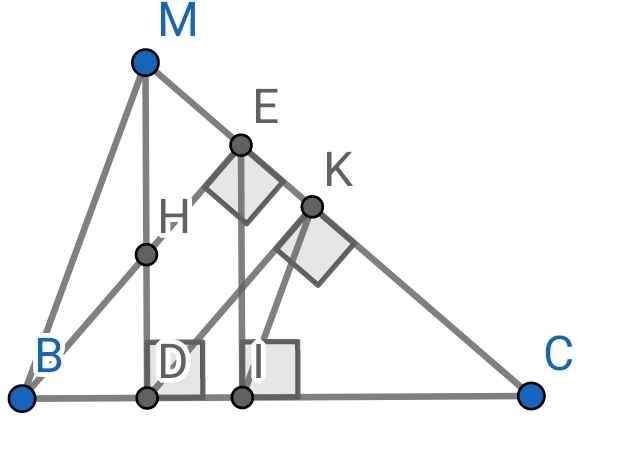
Cho tam giác ABC vuông tại A, AB < AC . M là điểm bất kì trên cạnh AC. Kẻ MD vuông góc với BC ( D thuộc BC ). Tam giác DMC đồng dạng với tam giác ABC.
Gọi E là giao điểm của AB với MD. C/m DB.DC = DE.DM.




a: Xét ΔCDM vuông tại D và ΔCAB vuông tại A có
\(\widehat{DCM}\) chung
Do đó: ΔCDM~ΔCAB
b: Xét ΔDCM vuông tại D và ΔDEB vuông tại D có
\(\widehat{DCM}=\widehat{DEB}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔDCM~ΔDEB
=>\(\dfrac{DC}{DE}=\dfrac{DM}{DB}\)
=>\(DC\cdot DB=DM\cdot DE\)