
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
Suy ra: AB/HB=BC/BA
hay \(AB^2=HB\cdot BC\)
b: Xét ΔHAC vuông tại H và ΔHBA vuông tại H có
\(\widehat{HAC}=\widehat{HBA}\)
Do đó; ΔHAC\(\sim\)ΔHBA
SUy ra: HA/HB=HC/HA
hay \(HA^2=HB\cdot HC\)
a) Xét ∆ABC(<A=90 ° ) và ∆HBA(<H=90 ° ), ta có:
<B chung ⟹∆ABC~ ∆HBA(g.g)
⟹AB/HB=BC/AB⟹AB*AB=HB*BC hay AB2=BH*BC
b)Xét ∆HAC(<H=90 °) và ∆HBA(<H=90 ° ), ta được:
<B=<HAC( vì cùng phụ với <BAH do <B+<BAH =90°; <HAC+<BAH =90°)
⟹∆HAC~∆HBA(g.g)
⟹HA/HB=HC/HA⟹HA*HA=HB*HC hayHA2=BH*CH

b: =>(x-1)(x+1)+4x(x-1)=0
=>(x-1)(5x+1)=0
=>x=1 hoặc x=-1/5
c: \(\Leftrightarrow2\left(6x+5\right)-10x-3=8x+4x+2\)
=>12x+10-10x-3=12x+2
=>-10x+7=2
=>-10x=-5
hay x=1/2

\(A=\left(x^2+3x+4\right)^2\)
ta có:
\(x^2+3x+4=x^2+2\cdot\dfrac{3}{2}x+\left(\dfrac{3}{2}\right)^2+\dfrac{7}{4}\\ =\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
vậy \(minA=\left(\dfrac{7}{4}\right)^2=\dfrac{49}{16}\Leftrightarrow x=-\dfrac{3}{2}\)

d: \(\Leftrightarrow\left(x+2\right)^2-\left(x-2\right)^2=8\)
\(\Leftrightarrow x^2+4x+4-x^2+4x-4=8\)
=>8x=8
hay x=1(nhận)
`(x+2)/(x-2)-(x-2)/(x+2)=8/(x^2-4)(x\ne+-2)`
`<=>(x+2)^2/((x-2)(x+2))-(x-2)^2/((x-2)(x+2))-8/((x-2)(x+2))=0`
`<=>(x^2+4x+4-x^2+4x-4-8)/((x-2)(x+2))=0`
`<=>(8x-8)/((x-2)(x+2))=0`
`=>8x-8=0<=>x=1`
Vậy `S={1}`

Bài 1:
Xét ΔDEF có
M là trung điểm của DE
P là trung điểm của DF
Do đó: MP là đường trung bình
=>MP//EF
=>ΔDMP\(\sim\)ΔDEF
Xét ΔDEF có
M là trung điểm của ED
N là trung điểm của FE
Do đó: MN là đường trung bình
=>ΔEMN\(\sim\)ΔEDF
Xét ΔDEF có
P là trung điểm của DF
N là trung điểm của EF
Do đó: PN là đường trung bình
=>PN//DE
hay ΔFPN\(\sim\)ΔFDE

Bài 5:
Theo đề, ta có:
\(\left(2x+5\right)^2-4x^2-12x=41\)
\(\Leftrightarrow20x-12x=41+25=66\)
hay \(x=8.25\left(m\right)\)
Chu vi là:
\(\left[\left(2\cdot8.25+5\right)^2+\left(4\cdot8.25^2+12\cdot8.25\right)\right]\cdot2=1667\left(m\right)\)


\(\dfrac{4x+2}{4x-2}+\dfrac{3-6x}{6x-6}\left(dkxd:x\ne\dfrac{1}{2};x\ne1\right)\)
\(=\dfrac{2\left(2x+1\right)}{2\left(2x-1\right)}+\dfrac{3\left(1-2x\right)}{6\left(x-1\right)}\)
\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2\left(x-1\right)}\)
\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2x-2}\)
\(=\dfrac{\left(2x+1\right)\left(2x-2\right)}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{\left(1-2x\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{4x^2-2x-2}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{4x^2-2x-2-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{2x-3}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{2x-3}{4x^2-6x+2}\)
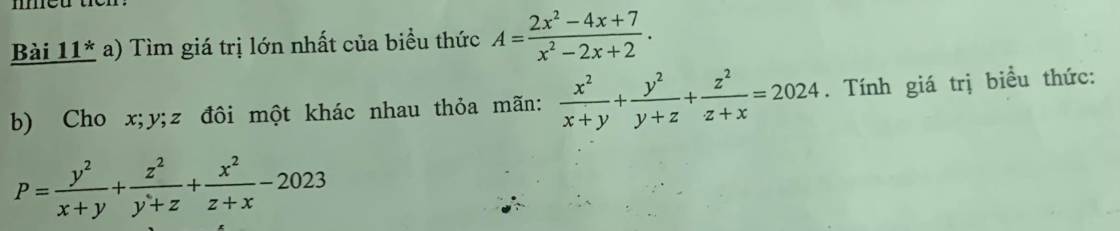





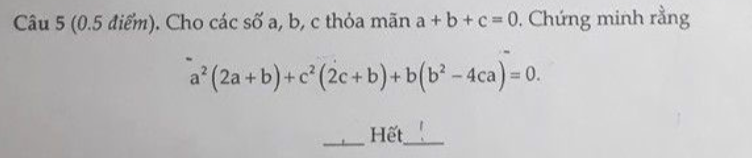

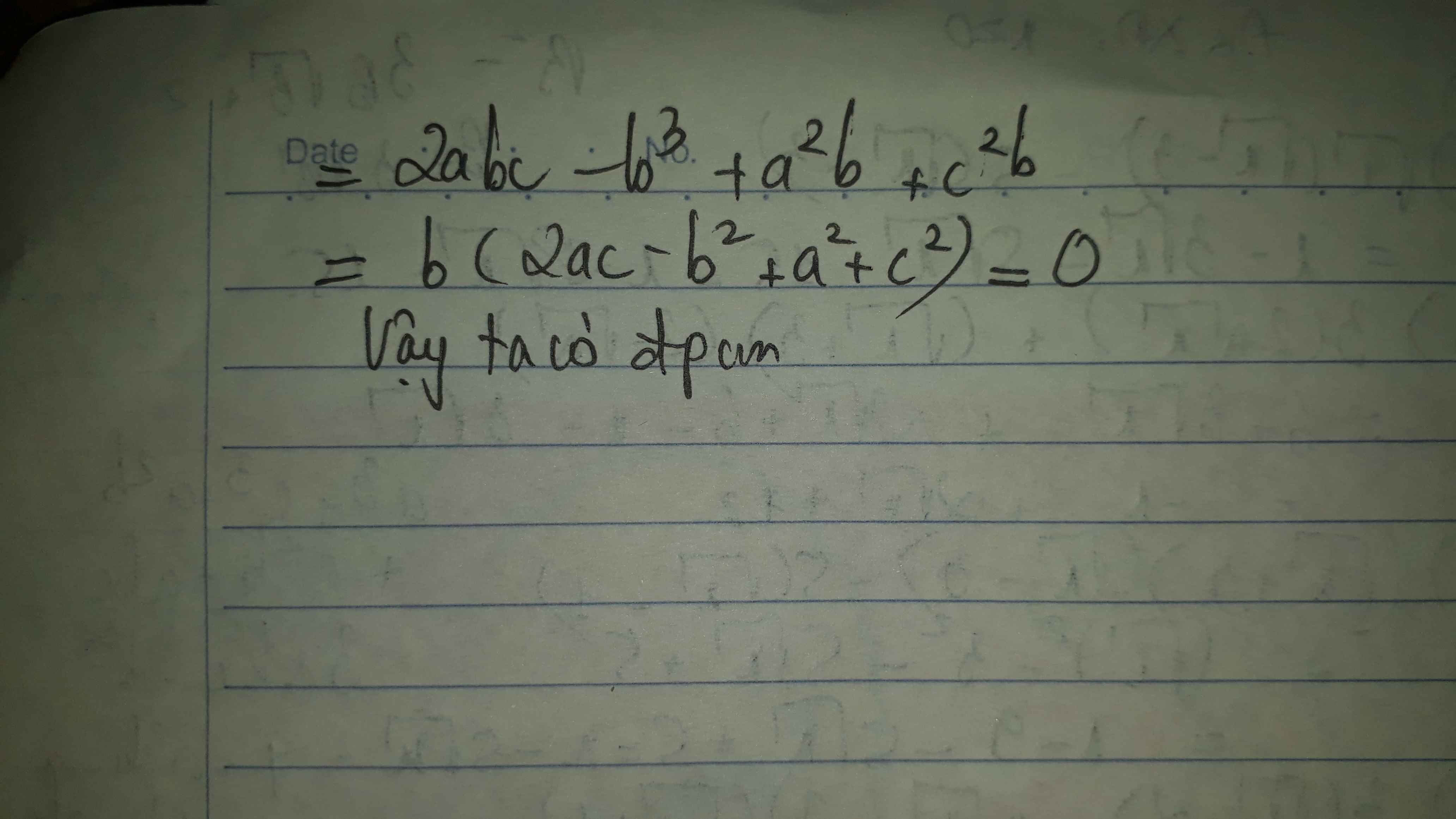
a: \(A=\dfrac{2x^2-4x+7}{x^2-2x+2}\)
\(=\dfrac{2x^2-4x+4+3}{x^2-2x+2}\)
\(=2+\dfrac{3}{x^2-2x+2}=2+\dfrac{3}{\left(x-1\right)^2+1}\)
\(\left(x-1\right)^2+1>=1\forall x\)
=>\(\dfrac{3}{\left(x-1\right)^2+1}< =\dfrac{3}{1}=3\forall x\)
=>\(A=\dfrac{3}{\left(x-1\right)^2+1}+2< =3+2=5\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1