a chứng minh rằng tổng của hai số tự nhiên lẻ liên tiếp là một số chia hết cho 4
b Chứng minh rằng nếu P và p + 2 là hai số nguyên tố lớn hơn 3 thì tổng của chúng chia hết cho 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{x+5}{2006}+\dfrac{x+6}{2005}+\dfrac{x+7}{2004}=-3\)
=>\(\left(\dfrac{x+5}{2006}+1\right)+\left(\dfrac{x+6}{2005}+1\right)+\left(\dfrac{x+7}{2004}+1\right)=-3+3=0\)
=>\(\dfrac{x+2011}{2006}+\dfrac{x+2011}{2005}+\dfrac{x+2011}{2004}=0\)
=>\(\left(x+2011\right)\left(\dfrac{1}{2006}+\dfrac{1}{2005}+\dfrac{1}{2004}\right)=0\)
=>x+2011=0
=>x=-2011

Để tính diện tích của hình thang BCED, chúng ta cần tìm chiều dài đáy lớn và chiều cao của hình thang.
Vì tứ giác BCED là hình thang, ta biết rằng đáy nhỏ BC và đáy lớn ED có độ dài bằng nhau. Gọi độ dài đáy lớn là x.
Theo định lý Pythagoras trong tam giác vuông ABC, ta tính được độ dài cạnh còn lại BC:
BC² = AB² + AC²
BC² = 60² + 80²
BC² = 3600 + 6400
BC = √10000
BC = 100 cm
Vì BC và ED là hai đường chéo của hình thang, nên chúng bằng nhau. Vậy x = 100 cm.
Để tính diện tích hình thang BCED, ta sử dụng công thức:
Diện tích = 0.5 * (đáy nhỏ + đáy lớn) * chiều cao
Diện tích = 0.5 * (BC + ED) * chiều cao
Diện tích = 0.5 * (100 + 100) * 30
Diện tích = 0.5 * 200 * 30
Diện tích = 3000 cm²
Vậy diện tích của hình thang BCED là 3000 cm².

a:Xét ΔABC có
BE,CF là các đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại D
Xét (O) có \(\widehat{AKB};\widehat{ACB}\) là các góc nội tiếp chắn cung AB
nên \(\widehat{AKB}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{AHE}\left(=90^0-\widehat{DAC}\right)\)
nên \(\widehat{AKB}=\widehat{AHE}\)
=>\(\widehat{AHK}=\widehat{AKH}\)
=>AK=AH
b: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{FEC}+\widehat{FBC}=180^0\)
mà \(\widehat{CEF}+\widehat{AEF}=180^0\)
nên \(\widehat{AEF}=\widehat{ABC}\)
Gọi Ax là tiếp tuyến tại A của (O)
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
DO đó: \(\widehat{xAC}=\widehat{ABC}\)
=>\(\widehat{xAC}=\widehat{AEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên FE//Ax
mà Ax\(\perp\)OA
nên OA\(\perp\)EF

Ta có:
\(56=2^3\cdot7\\ 84=2^2\cdot3\cdot7\\ 120=2^3\cdot5\cdot3\\=>ƯCLN\left(56;84;120\right)=2^2=4\)

\(2^{x+2}+2^{x+2}+2^{x+1}=224\\ =>2^{x+1}\cdot2+2^{x+1}\cdot2+2^{x+1}\cdot1=224\\ =>2^{x+1}\cdot\left(2+2+1\right)=224\\ =>2^{x+1}\cdot5=224\\ =>2^{x+1}=\dfrac{224}{5}\\ =>x+1=log_2\dfrac{224}{5}\\ =>x=log_2\dfrac{224}{5}-1\)

\(1,x^2+9-16y^2+6x\\ =\left(x^2+6x+9\right)-\left(4y\right)^2\\ =\left(x+3\right)^2-\left(4y\right)^2\\ =\left(x-4y+3\right)\left(x+4y+3\right)\\ 2,x^2-9+y^2+2xy\\ =\left(x^2+2xy+y^2\right)-9\\ =\left(x+y\right)^2-3^2\\ =\left(x+y-3\right)\left(x+y+3\right)\\ 3,x^2-4x+4-9y^2\\ =\left(x-2\right)^2-\left(3y\right)^2\\ =\left(x-3y-2\right)\left(x+3y-2\right)\\ 4,x^2-4xy+4y^2-81\\ =\left(x-2y\right)^2-9^2\\ =\left(x-2y-9\right)\left(x-2y+9\right)\\ 5,6x^2+6y^2-24+12xy\\ =\left(6x^2+12xy+6y^2\right)-24\\ =6\left[\left(x^2+2xy+y^2\right)-4\right]\\ =6\left[\left(x+y\right)^2-2^2\right]\\ =6\left(x+y-2\right)\left(x+y+2\right)\\ 6,9x^2-6x+1-25\\ =\left(3x-1\right)^2-5^2\\ =\left(3x-1-5\right)\left(3x-1+5\right)\\ =\left(3x-6\right)\left(3x+4\right)\)
7: \(x^2+4x+4-49y^2\)
\(=\left(x^2+4x+4\right)-49y^2\)
\(=\left(x+2\right)^2-49y^2\)
=(x+2+7y)(x+2-7y)
8: \(a^3+9a-ab^2-6a^2\)
\(=a\left(a^2-6a+9-b^2\right)\)
\(=a\left[\left(a-3\right)^2-b^2\right]\)
\(=a\left(a-3-b\right)\left(a-3+b\right)\)
9: \(8x^2-16x+8-32y^2\)
\(=8\left(x^2-2x+1-4y^2\right)\)
\(=8\left[\left(x-1\right)^2-\left(2y\right)^2\right]\)
=8(x-1-2y)(x-1+2y)
10: \(4x^2-4x+1-81a^2\)
\(=\left(4x^2-4x+1\right)-81a^2\)
\(=\left(2x-1\right)^2-\left(9a\right)^2\)
=(2x-1-9a)(2x-1+9a)
11: \(x^2-6xy+9y^2-121\)
\(=\left(x^2-6xy+9y^2\right)-121\)
\(=\left(x-3y\right)^2-11^2=\left(x-3y-11\right)\left(x-3y+11\right)\)
12: \(12x^2-24x+12-3y^2\)
\(=3\left(4x^2-8x+4-y^2\right)\)
\(=3\left[\left(2x-2\right)^2-y^2\right]=3\left(2x-2-y\right)\left(2x-2+y\right)\)

\(P=\dfrac{\left(x-1\right)^2+3}{\left(x-1\right)^2+5}=\dfrac{\left(x-1\right)^2+5-2}{\left(x-1\right)^2+5}=1-\dfrac{2}{\left(x-1\right)^2+5}\)
\(\left(x-1\right)^2+5>=5\forall x\)
=>\(\dfrac{2}{\left(x-1\right)^2+5}< =\dfrac{2}{5}\forall x\)
=>\(-\dfrac{2}{\left(x-1\right)^2+5}>=-\dfrac{2}{5}\forall x\)
=>\(P=\dfrac{-2}{\left(x-1\right)^2+5}+1>=-\dfrac{2}{5}+1=\dfrac{3}{5}\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1
\(Q=\dfrac{\left(2y+3\right)^2-3}{\left(2y+3\right)^2+4}=\dfrac{\left(2y+3\right)^2+4-7}{\left(2y+3\right)^2+4}=1-\dfrac{7}{\left(2y+3\right)^2+4}\)
\(\left(2y+3\right)^2+4>=4\forall y\)
=>\(\dfrac{7}{\left(2y+3\right)^2+4}< =\dfrac{7}{4}\forall y\)
=>\(-\dfrac{7}{\left(2y+3\right)^2+4}>=-\dfrac{7}{4}\forall y\)
=>\(Q=-\dfrac{7}{\left(2y+3\right)^2+4}+1>=-\dfrac{3}{4}\forall y\)
Dấu '=' xảy ra khi 2y+3=0
=>2y=-3
=>y=-3/2
\(F=\dfrac{\left(x-1\right)^2+5}{\left(x-1\right)^2+2}=\dfrac{\left(x-1\right)^2+2+3}{\left(x-1\right)^2+2}=1+\dfrac{3}{\left(x-1\right)^2+2}\)
\(\left(x-1\right)^2+2>=2\forall x\)
=>\(\dfrac{3}{\left(x-1\right)^2+2}< =\dfrac{3}{2}\forall x\)
=>\(F=\dfrac{3}{\left(x-1\right)^2+2}+1< =\dfrac{5}{2}\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1

\(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{x\left(x+1\right)}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}\\ =1+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3}\right)+...+\left(\dfrac{1}{x}-\dfrac{1}{x}\right)-\dfrac{1}{x+1}\\ =1-\dfrac{1}{x+1}\\ =\dfrac{x+1}{x+1}-\dfrac{1}{x+1}\\ =\dfrac{x}{x+1}\)
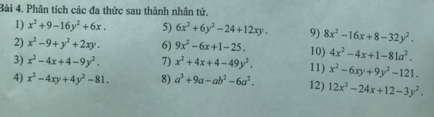
a) Hai số lẻ liên tiếp là : \(2k+1;2k+3\left(k\in Z\right)\)
Tổng 2 số trên là :
\(2k+1+2k+3=4k+4=4\left(k+1\right)⋮4\)
\(\Rightarrowđpcm\)