Giup mik voiii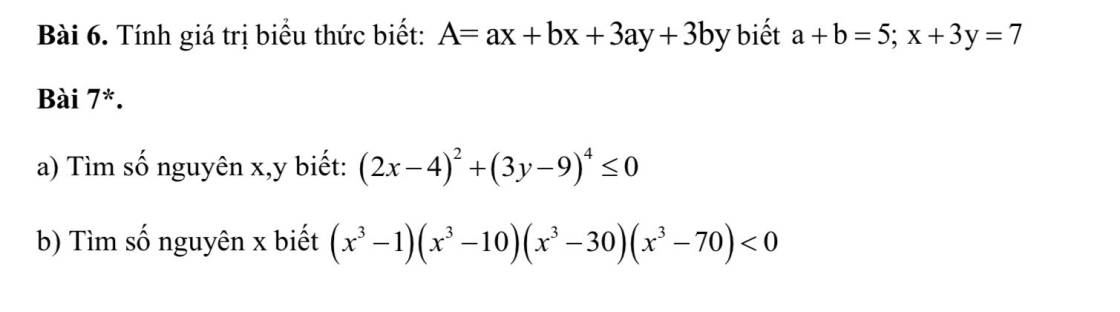
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(0,36\cdot4+36\%+2+2\cdot4\cdot0,18\)
\(=0,36\cdot4+0,18\cdot8+0,36+2\)
\(=0,36\cdot5+0,36\cdot4+2\)
\(=0,36\cdot9+2=2+3,24=5,24\)

Giải:
Gọi số tự nhiên nhỏ nhất cần tìm là \(x\); \(x\in\) N thì theo bài ra ta có:
Số thứ hai là: \(x\) + 1
Số thứ ba là: \(x+1+1\) = \(x\) + 2
Theo bài ra ta có: \(x\) + \(x\) + 1 + \(x\) + 2 = 183
(\(x\) + \(x\) + \(x\)) + (1 + 2) = 183
3\(x\) + 3 = 183
3\(x\) = 183 - 3
3\(x\) = 180
\(x\) = 180 : 3
\(x\) = 60
Vậy số tự nhiên nhỏ nhất thỏa mãn đề bài là: 60
Trung bình cộng của ba số là : 183:3=61
Vì trung bình cộng của ba số là số thứ hai.
Số nhỏ nhất là:61-1=60
Đáp số:60.

\(4,6.\left(168-120\right)+\left(2,1+2,5\right).\left(15+35\right)+\left(11,9-2,7\right)\)
\(=4,6.48+4,6.50+9,2\)
\(=4,6.48+4,6.50+4,6.2\)
\(=4,6.\left(48+50+2\right)\)
\(=4,6.100\)
\(=460\)

-36 : x = 30/7
x = -36 : 30/7
x = -42/5
--------
34/51 : x = 38/57
2/3 : x = 2/3
x = 2/3 : 2/3
x = 1

a: Chiều rộng là \(7,5\cdot\dfrac{3}{5}=4,5\left(m\right)\)
Diện tích xung quanh là \(\left(7,5+4,5\right)\cdot2\cdot3=6\cdot12=72\left(m^2\right)\)
b: Diện tích cần sơn là: \(72+7,5\cdot4,5=105,75\left(m^2\right)\)
Số tiền phải trả là:
\(105,75\cdot25000=2643750\left(đồng\right)\)

\(A=5+5^2+5^3+\dots+5^{200}\\5A=5^2+5^3+5^4+\dots+5^{201}\\5A-A=(5^2+5^3+5^4+\dots+5^{201})-(5+5^2+5^3+\dots+5^{200})\\4A=5^{201}-5\\\Rightarrow A=\frac{5^{201}-5}{4}\)
A = 5 + 5² + 5³ + ... + 5²⁰⁰
⇒ 5A = 5² + 5³ + 5⁴ + ... + 5²⁰¹
⇒ 4A = 5A - A
= (5² + 5³ + 5⁴ + ... + 5²⁰¹) - (5 + 5² + 5³ + ... + 5²⁰⁰)
= 5²⁰¹ - 5
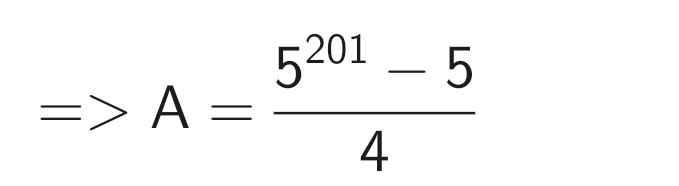

\(3\cdot53\cdot8+4\cdot6\cdot87-212\cdot40\)
\(=24\cdot53+24\cdot87-212\cdot40\)
\(=24\cdot\left(53+87\right)-212\cdot40\)
\(=24\cdot140-212\cdot40=-5120\)

\(27\cdot38+27\cdot62\)
\(=27\left(38+62\right)=27\cdot100=2700\)
Bài 6:
\(A=ax+bx+3ay+3by\)
\(=x\left(a+b\right)+3y\left(a+b\right)\)
\(=\left(a+b\right)\left(x+3y\right)=5\cdot7=35\)
Bài 7:
a: \(\left(2x-4\right)^2>=0\forall x\)
\(\left(3y-9\right)^4>=0\forall y\)
Do đó: \(\left(2x-4\right)^2+\left(3y-9\right)^4>=0\forall x,y\)
mà \(\left(2x-4\right)^2+\left(3y-9\right)^4< =0\forall x,y\)
nên \(\left\{{}\begin{matrix}2x-4=0\\3y-9=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
b; (\(x^3\) - 1)(\(x^3\) - 10)(\(x^3\) - 30)(\(x^3\) - 70) < 0
Đặt \(x^3\) = t
Khi đó: T = (t - 1)(t - 10)(t - 30)(t - 70) < 0
Lập bảng xét dấu ta có:
Theo bảng trên ta có:
1 < t < 10 hoặc 30 < t < 70
⇒ 1 < \(x^3\) - 1 < 10 ⇒ 2 < \(x^3\) < 11
Vì \(x\) nguyên nên \(x\)3 = 8 ⇒ \(x^3\) = 23 ⇒ \(x=2\)
30 < t < 70
30 < \(x^3\) - 1 < 70
31 < \(x^3\) < 71
Vì \(x\) nguyên nên \(x^3\) = 64
⇒ \(x^3\) = 43 ⇒ \(x\) = 4
Vậy \(x\) \(\in\) {2; 4}