
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{2}{3}a=\dfrac{3}{5}b=\dfrac{6}{7}c\)
=>\(\dfrac{a}{\dfrac{3}{2}}=\dfrac{b}{\dfrac{5}{3}}=\dfrac{c}{\dfrac{7}{6}}\)
mà a+b+c=1950
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{3}{2}}=\dfrac{b}{\dfrac{5}{3}}=\dfrac{c}{\dfrac{7}{6}}=\dfrac{a+b+c}{\dfrac{3}{2}+\dfrac{5}{3}+\dfrac{7}{6}}=\dfrac{1950}{\dfrac{13}{3}}=450\)
=>\(\left\{{}\begin{matrix}a=450\cdot\dfrac{3}{2}=675\\b=450\cdot\dfrac{5}{3}=750\\c=450\cdot\dfrac{7}{6}=525\end{matrix}\right.\)

2 giờ rưỡi=2,5 giờ
Thời gian dự định đi nhiều hơn thời gian thực là:
3 giờ - 2,5 giờ= 0,5 giờ
Quãng đường ô tô đi với vận tốc tăng thêm là:
9 x 2,5= 22,5 km
Vận tốc thực ô tô đi là:
22,5 : 0,5 =45 km/giờ
Quãng đường AB dài là:
(45 + 9) x 2,5 = 135 km
Đáp số:135 km

Diện tích một mặt của hình lập phương là :
384 : 6 = 64 ( cm2 )
Ta có : 64 = 8. 8
Nên cạnh của hình lập phương là 8 cm
Đáp số : 8 cm
Học tốt nha
Độ dài cạnh của hình lập phương là:
\(\sqrt{\dfrac{384}{6}}=8\left(cm\right)\)
=>Chọn C

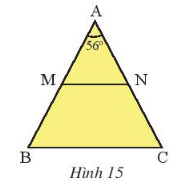
a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-50^0}{2}=65^0\)
b: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC(ΔABC cân tại A)
nên AM=MB=AN=NC
Xét ΔAMN có AM=AN
nên ΔAMN cân tại A
c: Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC

ĐKXĐ: n<>-1/5
Để \(\dfrac{4n-12}{5n+1}\) nguyên thì \(4n-12⋮5n+1\)
=>\(20n-60⋮5n+1\)
=>\(20n+4-64⋮5n+1\)
=>\(-64⋮5n+1\)
=>\(5n+1\in\left\{1;-1;2;-2;4;-4;8;-8;16;-16;32;-32;64;-64\right\}\)
=>\(n\in\left\{0;-\dfrac{2}{5};\dfrac{1}{5};-\dfrac{3}{5};\dfrac{3}{5};-1;\dfrac{7}{5};-\dfrac{9}{5};3;-\dfrac{17}{5};\dfrac{31}{5};-\dfrac{33}{5};\dfrac{63}{5};-13\right\}\)
mà n nguyên
nên \(n\in\left\{0;-1;3;-13\right\}\)

Trung bình cộng của ba số a,b,c là 270
=>\(a+b+c=270\cdot3=810\)
\(A=\left(a+c\right)\cdot2-270\cdot5+2\cdot b\)
\(=2\left(a+b+c\right)-1350\)
\(=2\cdot810-1350=270\)

=1/2(1/2+1/6+1/12+1/20+...+1/90)
=1/2(1-1/2+1/2-1/3+...+1/9-1/10)
=1/2*9/10=9/20

1: Xét ΔCFE vuông tại F và ΔCAB vuông tại A có
\(\widehat{FCE}\) chung
Do đó: ΔCFE~ΔCAB
=>\(\dfrac{CF}{CA}=\dfrac{CE}{CB}\)
=>\(\dfrac{CF}{CE}=\dfrac{CA}{CB}\)
=>\(CF\cdot CB=CA\cdot CE\)
2: Xét ΔCFA và ΔCEB có
\(\dfrac{CE}{CE}=\dfrac{CA}{CB}\)
\(\widehat{FCA}\) chung
Do đó: ΔCFA~ΔCEB
=>\(\widehat{CAF}=\widehat{CBE}\)
3: Xét ΔEHA vuông tại H và ΔEAB vuông tại A có
\(\widehat{HEA}\) chung
Do đó: ΔEHA~ΔEAB
=>\(\dfrac{EH}{EA}=\dfrac{EA}{EB}\)
=>\(EA^2=EH\cdot EB\)
mà EA=EC
nên \(CE^2=EH\cdot EB\)