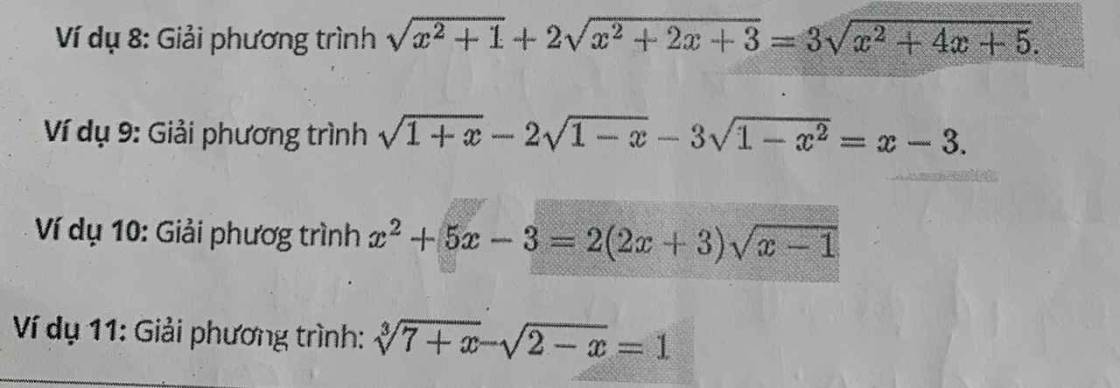giúp vs ạ
giúp vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(x^2=t\left(t\ge0\right)\)
Khi đó pt đã cho trở thành \(t^2-2mt-\left(2m-3\right)=0\) (*)
a) Để pt có 4 nghiệm thì (*) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\S>0\\P>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-m\right)^2-\left[-\left(2m-3\right)\right]>0\\2m>0\\3-2m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+2m-3>0\\m>0\\m< \dfrac{3}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(m+3\right)>0\\m>0\\m< \dfrac{3}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>1\\m< -3\end{matrix}\right.\\m>0\\m< \dfrac{3}{2}\end{matrix}\right.\)
\(\Leftrightarrow1< m< \dfrac{3}{2}\)
Vậy \(1< m< \dfrac{3}{2}\)
b) Để pt vô nghiệm thì pt (*) vô nghiệm hoặc có 2 nghiệm âm phân biệt.
TH1: (*) vô nghiệm \(\Leftrightarrow\Delta'< 0\) \(\Leftrightarrow-3< m< 1\)
TH2: (*) có 2 nghiệm âm phân biệt \(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\S< 0\\P>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -3\\m>1\end{matrix}\right.\\m< 0\\m< \dfrac{3}{2}\end{matrix}\right.\)
\(\Leftrightarrow m< -3\)
Vậy \(m< -1\) và \(m\ne-3\)

cứ mỗi đỉnh của đa giác thì sẽ tạo ra được 1 tam giác có 2 cạnh là 2 cạnh của đa giác. Mà đa giác có 10 đỉnh nên ta sẽ 10 tam giác thoả yêu câu

Gọi chữ số cần lập có dạng
- Nếu các chữ số không yêu cầu đôi một khác nhau:
có 4 cách chọn, có 6 cách chọn; 3 vị trí còn lại đều có 7 cách chọn
có số
- Nếu các chữ số đôi một khác nhau:
+ Nếu : có 6 cách chọn, b có 5 cách chọn, c có 4 cách chọn, d có 3 cách chọn có số
+ Nếu có 3 cách chọn, a có 5 cách chọn, b có 5 cách chọn, c có 4 cách chọn, d có 3 cách chọn số
có số
Lời giải:
Gọi số tự nhiên có 5 chữ số khác nhau là $\overline{abcde}$
Số cách lập số tự nhiên có 5 chữ số khác nhau từ 2,3,4,5,6 là: $5!=120$ số
Số cách lập số tự nhiên có 5 chữ số khác nhau từ 2,3,4,5,6 mà chia hết cho 5 là:
$4!.1=24$ số (do e chỉ có 1 cách chọn là số 5, 4 số còn lại hoán vị là 4!)
Số cách lập số tự nhiên có 5 chữ số khác nhau mà không chia hết cho 5:
$120-24=96$ (số)

Gọi chữ số cần lập có dạng
- Nếu các chữ số không yêu cầu đôi một khác nhau:
có 4 cách chọn, có 6 cách chọn; 3 vị trí còn lại đều có 7 cách chọn
có số
- Nếu các chữ số đôi một khác nhau:
+ Nếu : có 6 cách chọn, b có 5 cách chọn, c có 4 cách chọn, d có 3 cách chọn có số
+ Nếu có 3 cách chọn, a có 5 cách chọn, b có 5 cách chọn, c có 4 cách chọn, d có 3 cách chọn số
có số


8.
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+2x+3}=a>0\\\sqrt{x^2+4x+5}=b>0\end{matrix}\right.\) \(\Rightarrow2a^2-b^2=x^2+1\)
Pt trở thành:
\(\sqrt{2a^2-b^2}+2a=3b\)
\(\Leftrightarrow\sqrt{2a^2-b^2}=3b-2a\)
\(\Rightarrow2a^2-b^2=4a^2-12ab+9b^2\)
\(\Leftrightarrow2a^2-12ab+10b^2=0\Rightarrow\left[{}\begin{matrix}a=b\\a=5b\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2+2x+3}=\sqrt{x^2+4x+5}\\\sqrt{x^2+2x+3}=5\sqrt{x^2+4x+5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+2x+3=x^2+4x+5\\x^2+2x+3=25\left(x^2+4x+5\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\24x^2+98x+122=0\left(vn\right)\end{matrix}\right.\)
9.
ĐKXĐ: \(-1\le x\le1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{1+x}=a\ge0\\\sqrt{1-x}=b\ge0\end{matrix}\right.\) \(\Rightarrow a^2+2b^2=3-x=-\left(x-3\right)\)
Pt trở thành:
\(a-2b-3ab=-\left(a^2+2b^2\right)\)
\(\Leftrightarrow a-2b+a^2-3ab+2b^2=0\)
\(\Leftrightarrow a-2b+\left(a-b\right)\left(a-2b\right)=0\)
\(\Leftrightarrow\left(a-2b\right)\left(a-b+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=2b\\a+1=b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{1+x}=2\sqrt{1-x}\\\sqrt{1+x}+1=\sqrt{1-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}1+x=4\left(1-x\right)\\x+2+2\sqrt{1+x}=1-x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=3\Rightarrow x=\dfrac{3}{5}\\-1-2x=2\sqrt{1+x}\left(1\right)\end{matrix}\right.\)
Xét (1) \(\Leftrightarrow\left\{{}\begin{matrix}-1-2x\ge0\\\left(-1-2x\right)^2=4\left(1+x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\x^2=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow x=-\dfrac{\sqrt{3}}{2}\)
Vậy \(x=\left\{\dfrac{3}{5};-\dfrac{\sqrt{3}}{2}\right\}\)