Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chia 16 số ra làm 3 tập:
A={1;4;7;10;13;16}; B={2;5;8;11;14}; C={3;6;9;12;15}
TH1: 1 số trong A, 1 số trong B, 1 số trong C
=>Có 6*5*5=150 cách
TH2: 3 số trong A
=>Có \(C^3_6=20\left(cách\right)\)
TH3: 3 số trong B hoặc C
=>Có \(C^3_5\cdot2=20\left(cách\right)\)
=>n(A)=20+20+150=190
\(n\left(omega\right)=C^3_{16}=560\)
=>P(A)=19/56

Ta thấy hai biến cố :”Hai quả bóng lây ra cùng màu” và “Hai quả bóng lấy ra khác màu” là hai biến cố đối
Suy ra xác suất của biến cố “Hai quả bóng lây ra cùng màu” là \(1 - 0,6 = 0,4\)

Gọi số quýt ban đầu ở mỗi rổ là x (quả)
Muốn lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở mỗi rổ lúc đầu phải nhiều hơn 30 quả hay x > 30.
Khi đó rổ thứ nhất còn x – 30 quả; rổ thứ hai có x + 30 quả.
Vì số quả ở rổ thứ hai bằng 1/3 bình phương số quả còn lại ở rổ thứ nhất nên ta có phương trình:
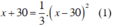
Giải phương trình (1):
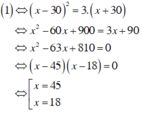
Vì x > 30 nên x = 45 thỏa mãn.
Vậy ban đầu mỗi rổ có 45 quả cam.

Cách 1: x = n 1 x 1 + n 2 x 2 + n 3 x 3 + n 4 x 4 + n 5 x 5 n = 4 . 6 + 3 . 7 + 5 . 8 + 9 . 9 + 6 . 10 30 ≈ 8 , 33
Cách 2: Sử dụng máy tính Casio fx - 570 VNPLUS
+ Nhập ![]() (vào chế độ thống kê).
(vào chế độ thống kê).
+ Nhập ![]() (hiển thị cột tần số).
(hiển thị cột tần số).
+ Nhập ![]() (nhập giá trị).
(nhập giá trị).
+ Nhập ![]() , sau đó ấn
, sau đó ấn ![]() .
.
+ Tính giá trị trung bình: Ấn ![]()
⇒ x = 8 , 3333333 …
Đáp án A.

a) Ta có: Vận tốc đầu ở đỉnh dốc = 0 ( v0= 0) quả cầu chuyển động nhanh dần đều
S = 0 + (1/2).a.t²
=> a = 2.S/t²
= 2.100/10²
= 2 m/s²
ta có:
- Quả cầu nằm ngang trên mặt phẳng và chuyển động chậm dần với gia tốc a'
- Tốc độ đầu v là tốc độ tại chân dốc, tốc độ cuối = 0
v = 0 + a.t
= 0 + 2.10
= 20 (m/s)
Ta lại có: 0² - v² = 2.a'S
=> a' = -v²/2S
= - 20²/2.50
= - 4 (m/s²) ( vật chuyển động chậm dần đều )
b) Thời gian mà vật chuyển động trên mặt phẳng ngang t' là:
0 = v - a't'
=> t' = v/a' = 20/4 = 5 (s)
Thời gian quả cầu chuyển động trong cả quá trình là:
t + t' = 10 + 5 = 15 (s)
a)* Từ đỉnh dốc vận tốc đầu = 0, quả cầu chuyển động nhanh dần
S = 0 + (1/2)at²
=> a = 2S/t² = 2*100/10² = 2 m/s²
*Trên mặt phẳng ngang quả cầu chuyển động chậm dần với gia tốc a', tốc độ đầu v là tốc độ tại chân dốc, tốc độ cuối = 0
v = 0+at = 0 + 2.10 = 20 m/s
Có: 0² - v² = 2.a'S
=> a' = -v²/2S = -20²/2.50 = -4 (m/s²) (dấu - chứng tỏ vật cđộng chậm dần)
b) thời gian chuyển động trên mặt phẳng ngang: t'
0 = v - a't' => t' = v/a' = 20/4 = 5s
thời gian của cả quá trình chuyển động: t + t' = 10 + 5 = 15s
Chúc bạn học tốt !!!

Tham khảo:
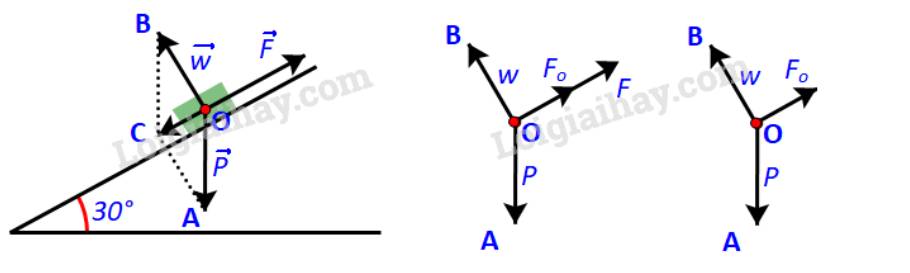
Khẩu pháo chịu tác động của ba lực: trọng lực \(\overrightarrow P \)(kí hiệu \(\overrightarrow {OA} \)), phản lực \(\overrightarrow w \)(kí hiệu \(\overrightarrow {OB} \)) và lực kéo \(\overrightarrow F \). Để kéo pháo thì độ lớn của lực kéo phải lớn hơn độ lớn của lực kéo khi pháo cân bằng \(\overrightarrow {{F_o}} \)(kí hiệu \(\overrightarrow {O{F_o}} \) )
Khi pháo cân bằng thì: \(\overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow 0 \)
Để tổng hợp lực \(\overrightarrow P \) và \(\overrightarrow w \), ta vẽ hình bình hành OACB.
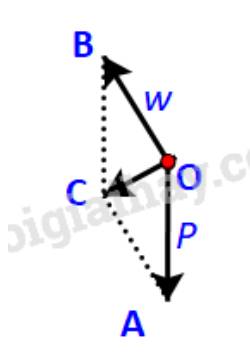
Ta có:
\(OB = \;AC;\;\;OB//\;AC\;\; \Rightarrow \overrightarrow {OB} = \;\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {OB} + \overrightarrow {OA} = \overrightarrow {AC} + \overrightarrow {OA} = \overrightarrow {OA} + \overrightarrow {AC} = \overrightarrow {OC} \)
\( \Rightarrow \overrightarrow 0 = \overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {O{F_o}} = \overrightarrow {OC} + \overrightarrow {O{F_o}} \)
\( \Rightarrow \;O\) là trung điểm của \(C{F_o}\), hay \(OC = \left| {\overrightarrow {{F_o}} } \right|\).
Lại có: \(OB \bot \;\;OC\)(do \(\overrightarrow {OB} \) là phản lực)
\( \Rightarrow \;AC \bot CO \Rightarrow OC = OA\,.\,\,\cos \widehat {AOC}\)
Mà \(\widehat {AOC} = {90^o} - {30^o} = {60^o}\); \(\left| {\overrightarrow P } \right| = OA = 22\;148\;N\)
\( \Rightarrow OC = 22\;148\,.\,\,\cos {60^o} = 11074\;\left( N \right)\)
Vậy lực \(\overrightarrow {{F_o}} \)có độ lớn là \(11\;074\;N\), để kéo pháo thì lực \(\overrightarrow F \) cùng hướng với \(\overrightarrow {{F_o}} \) và \(\left| {\overrightarrow F } \right| > 11\;074\;N\)
Vì \(11\;074\;:100 = 110,74\) nên cần tối thiểu 111 người để kéo pháo.