Rất rõ ràng là câu A nhé bạn, vì \(O\in AC\subset\left(SAC\right)\)

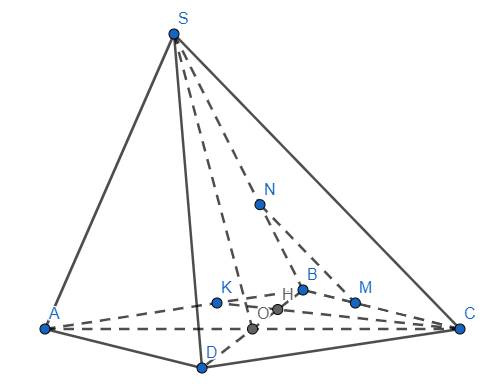
a) Ta có \(\left\{{}\begin{matrix}S\subset\left(SAC\right)\\S\subset\left(SBD\right)\end{matrix}\right.\)

và \(\left\{{}\begin{matrix}O\in AC\subset\left(SAC\right)\\O\in BD\subset\left(SBD\right)\end{matrix}\right.\) nên SO chính là giao tuyến của (SAC) và (SBD)

b) Trong mp(ABCD) cho CK cắt BD tại H. Do \(BD\subset\left(SBD\right)\) nên H cũng là giao điểm của CK và (SBD).

c) Vì \(\dfrac{BN}{NS}=\dfrac{BM}{MC}=\dfrac{1}{2}\) \(\Rightarrow\) MN//SC (Thelas đảo)

\(\Rightarrow\) MN//(SAC)

1

1

Lời giải:

Gọi $X$ là biến cố sinh viên là nữ và $Y$ là biến cố sinh viên học ngành A.

Theo bài ra ta có:

$P(X)=0,52; P(Y) = 0,05; P(XY)=0,02$
a. 

Xác suất sinh viên là nữ nếu sinh viên học ngành A là:
$P(X|Y) = \frac{P(XY)}{P(Y)}=\frac{0,02}{0,05}=\frac{2}{5}$

b. 

Xác suất sinh viên học ngành A biết sinh viên là nữ là:

$P(Y|X) = \frac{P(XY)}{P(X)}=\frac{0,02}{0,52}=\frac{1}{26}$

Lời giải:

Gọi $S=\frac{1}{5}+\frac{1}{5^2}+...+\frac{1}{5^n}$

$5S=1+\frac{1}{5}+....+\frac{1}{5^{n-1}}$

$\Rightarrow 4S=5S-S=1-\frac{1}{5^n}$

$S=\frac{1}{4}-\frac{1}{4.5^n}$

Khi $n\to \infty$ thì $4.5^n\to \infty\Rightarrow \frac{1}{4.5^n}\to 0$

$\Rightarrow \lim S = \frac{1}{4}-\lim \frac{1}{4.5^n}=\frac{1}{4}$