
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bổ sung đề. ∆ABC cân tại A
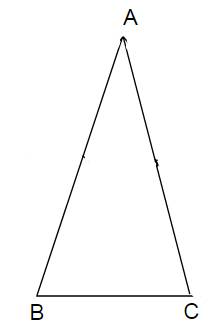
a) Do ∆ABC cân tại A (gt)
⇒ ∠C = ∠B = 70⁰
Ta có:
∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠A = 180⁰ - (∠B + ∠C)
= 180⁰ - (70⁰ + 70⁰)
= 40⁰
b) Do ∆ABC cân tại A (gt)
⇒ ∠B = ∠C = 50⁰
Ta có:
∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠A = 180⁰ - (∠B + ∠C)
= 180⁰ - (50⁰ + 50⁰)
= 80⁰
c) Do ∆ABC cân tại A (gt)
⇒ ∠B = ∠C
Ta có:
∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠B + ∠C = 180⁰ - ∠A
= 180⁰ - 80⁰
= 100⁰
Mà ∠B = ∠C (cmt)
⇒ ∠B = ∠C = 100⁰ : 2 = 50⁰

Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(AB=AC\) (vì là hai cạnh bên trong tam giác cân)
\(\widehat{ABD}=\widehat{ACE}\) (vì là hai góc ở đáy trong tam giác cân)
\(BD=CE\left(gt\right)\)
\(\Rightarrow\Delta ABD=\Delta ACE\left(c.g.c\right)\)
\(\Rightarrow AD=AE\) (2 cạnh tương ứng)
Hay ΔADE cân tại A
Do ∆ABC cân tại A (gt)
⇒ AB = AC và ∠B₁ = ∠C₁
Xét ∆ABD và ∆ACE có:
AB = AC (cmt)
∠B₁ = ∠C₁ (cmt)
BD = CE (gt)
⇒ ∆ABD = ∆ACE (c-g-c)
⇒ AD = AE (hai cạnh tương ứng)
⇒ ∆ADE cân tại A

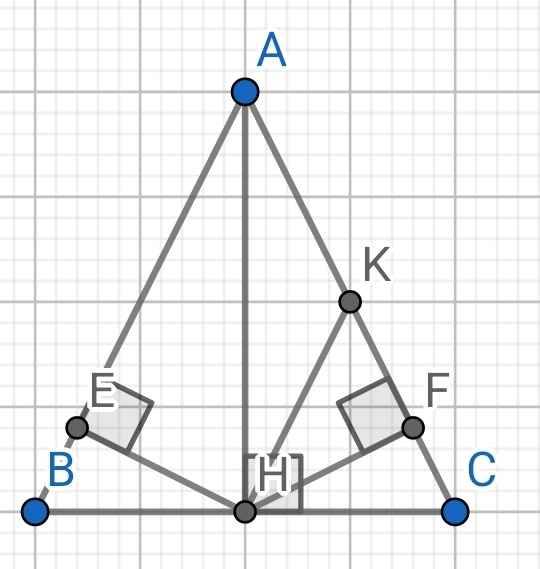
a) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB và AB = AC
Do ∠ABC = ∠ACB (cmt)
⇒ ∠ABH = ∠ACH
Xét hai tam giác vuông: ∆ABH và ∆ACH có:
AB = AC (cmt)
∠ABH = ∠ACH (cmt)
⇒ ∆ABH = ∆ACH (cạnh huyền - góc nhọn)
b) Do ∆ABH = ∆ACH (cmt)
⇒ BH = CH (hai cạnh tương ứng)
Do ∠ABH = ∠ACH (cmt)
⇒ ∠EBH = ∠FCH
Xét hai tam giác vuông: ∆EBH và ∆FCH có:
BH = CH (cmt)
∠EBH = ∠FCH (cmt)
⇒ ∆EBH = ∆FCH (cạnh huyền - góc nhọn)
⇒ EB = FC (hai cạnh tương ứng)
c) Do HK // AB (gt)
⇒ ∠KHC = ∠ABC (đồng vị)
Mà ∠ABC = ∠ACB (cmt)
⇒ ∠KHC = ∠ACB
⇒ ∠KHC = ∠KCH
⇒ ∆KCH cân tại K
⇒ KH = KC (1)
Do ∆ABH = ∆ACH (cmt)
⇒ ∠BAH = ∠CAH (hai góc tương ứng)
⇒ ∠BAH = ∠KAH
Do HK // AB (gt)
⇒ ∠KHA = ∠BAH (so le trong)
Mà ∠BAH = ∠KAH (cmt)
⇒ ∠KHA = ∠KAH
⇒ ∆KAH cân tại K
⇒ KA = KH (2)
Từ (1) và (2) ⇒ KA = KC
Hay K là trung điểm của AC

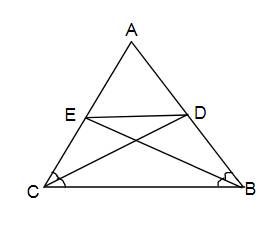
a: Ta có: \(\widehat{ABD}=\widehat{DBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\widehat{ECB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABD}=\widehat{DBC}=\widehat{ACE}=\widehat{ECB}\)
Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
b: Xét ΔABC có \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
nên DE//BC
c: Sửa đề: BE=ED=DC
Ta có: ED//BC
=>\(\widehat{EDB}=\widehat{DBC}\)(hai góc so le trong)
mà \(\widehat{DBC}=\widehat{EBD}\)(BD là phân giác của góc EBC)
nên \(\widehat{EDB}=\widehat{EBD}\)
=>ΔEBD cân tại E
=>EB=ED
Ta có: AE+EB=AB
AD+DC=AC
mà AE=AD
và AB=AC
nên EB=DC
=>BE=ED=DC

Lời giải:
Sử dụng bổ đề: Một số chính phương khi chia 3 dư 0 hoặc 1.
Chứng minh:
Nêú chia hết cho thì (dư )
Nếu không chia hết cho . Khi đó
chia dư
Vậy ta có đpcm
-----------------------------
Áp dụng vào bài:
TH1: Nếu chia hết cho thì hiển nhiên
TH1: Nếu
chia dư
TH3: Nếu
chia dư
TH4: Nếu
chia dư
đây bạn

Ta có: \(A=\dfrac{2023}{x^{2022}+2023}+2022\)
Lại có: \(x^{2022}\ge0\forall x\)
\(\Leftrightarrow x^{2022}+2023\ge2023\forall x\)
\(\Leftrightarrow\dfrac{1}{x^{2022}+2023}\le\dfrac{1}{2023}\forall x\)
\(\Leftrightarrow\dfrac{2023}{x^{2022}+2023}+2022\le\dfrac{2023}{2023}+2022=2023\forall x\)
\(\Leftrightarrow A\le2023\forall x\)
Dấu \("="\) xảy ra khi: \(x^{2022}=0\Leftrightarrow x=0\)
Vậy \(Max_A=2023\) tại \(x=0\).
Biểu thức lớn nhất khi và chỉ khi nhỏ nhất.
Ta có: với mọi . Dấu bằng xảy ra khi và chỉ khi .
Vậy khi , đạt giá trị lớn nhất bằng .

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE
Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBF}\) chung
Do đó: ΔBEF=ΔBAC
=>BF=BC
=>ΔBFC cân tại B
c: Ta có: ΔBFC cân tại B
mà BD là đường phân giác
nên BD là đường trung tuyến của ΔBCF
| GT |
là phân giác của góc
|
| KL |
a) . b) cân tại . c) là đường trung tuyesn của . |
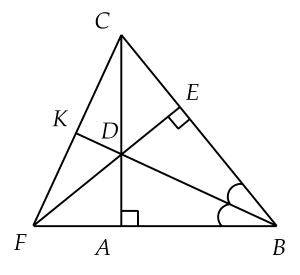
a) Xét và lần lượt vuông tại và .
chung.
( là tia phân giác).
Suy ra (cạnh huyền - góc nhọn).
b) Vì phần a) nên (2)
Xét vuông tại và vuông tại có:
(đối đỉnh)
Suy ra (cạnh góc vuông - góc nhọn)
Nên (2).
Từ (1) và (2) suy ra
Hay
Vậy cân tại .
c) Giả sử kéo dài cắt tại
Xét và có:
là cạnh chung
(Vì là phân giác của )
( chứng minh phần
Suy ra c.g.c
Suy ra (hai cạnh tương ứng)
Vậy hay là đường trung tuyến của .

a) P(x) = 2x³ - 3x + 5x² + 2 + x
= 2x³ + 5x² + (-3x + x) + 2
= 2x³ + 5x² - 2x + 2
Q(x) = -x³ - 3x² + 2x + 6 - 2x²
= -x³ + (-3x² - 2x²) + 2x + 6
= -x³ - 5x² + 2x + 6
b) P(x) + Q(x) = (2x³ + 5x² - 2x + 2) + (-x³ - 5x² + 2x + 6)
= 2x³ + 5x² - 2x + 2 - x³ - 5x² + 2x + 6
= (2x³ - x³) + (5x² - 5x²) + (-2x + 2x) + (2 + 6)
= x³ + 8
P(x) - Q(x) = (2x³ + 5x² - 2x + 2) - (-x³ - 5x² + 2x + 6)
= 2x³ + 5x² - 2x + 2 + x³ + 5x² - 2x - 6
= (2x³ + x³) + (5x² + 5x²) + (-2x - 2x) + (2 - 6)
= 3x³ + 10x² - 4x - 4

a) Tập hợp M:
M={xanh; đỏ; vàng; da cam; tím; trắng; hồng}
b) Xác xuất để biêna cố trên xảy ra là:
`P=1/7`
a) Tập hợp gồm các kết quả có thể xảy ra khi bút màu được rút ra là:
xanh, đỏ, vàng, da cam, tím, trắng, hồng .
b) Số phần tử của tập hợp là .
Xác suất biến cố "Màu được rút ra là vàng" là:
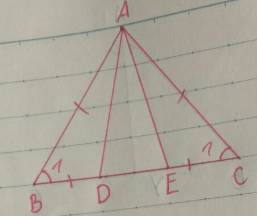
Đặt \(\dfrac{x}{-4}=\dfrac{y}{-7}=\dfrac{z}{3}=k\)
=>\(x=-4k;y=-7k;z=3k\)
\(A=\dfrac{-2x+y+3z}{2x-3y-6z}\)
\(=\dfrac{-2\cdot\left(-4k\right)+\left(-7k\right)+3\cdot3k}{2\cdot\left(-4k\right)-3\cdot\left(-7k\right)-6\cdot3k}\)
\(=\dfrac{8k-7k+9k}{-8k+21k-18k}\)
\(=\dfrac{10}{-26+21}=-2\)