\(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{2023\cdot2024}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\\ =1-\dfrac{1}{2024}\\ =\dfrac{2023}{2024}\\ B=\dfrac{4}{2\cdot4}+\dfrac{4}{4\cdot6}+...+\dfrac{4}{2022\cdot2024}\\ =2\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{2022\cdot2024}\right)\\ =2\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2022}-\dfrac{1}{2024}\right)\\ =2\left(\dfrac{1}{2}-\dfrac{1}{2024}\right)\\ =2\left(\dfrac{1012-1}{2024}\right)=\dfrac{1011}{1012}\)

\(A=\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2023.2024}\\ A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2023}-\dfrac{1}{1024}\\ A=1-\dfrac{1}{2024}=\dfrac{2023}{2024}\)

\(B=\dfrac{4}{2.4}+\dfrac{4}{4.6}+...+\dfrac{4}{2022.2024}\\ B=2\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2022}-\dfrac{1}{2024}\right)\\ B=2\left(\dfrac{1}{2}-\dfrac{1}{2024}\right)=\dfrac{2.1011}{2024}=\dfrac{1011}{1012}\)

sửa đề ý B nhé

a) 

\(3,5x-2=\dfrac{1}{3}x+\dfrac{2}{7}\\ \Leftrightarrow\dfrac{7}{2}x-\dfrac{1}{3}x=\dfrac{2}{7}+2\\ \Leftrightarrow x\left(\dfrac{7}{2}-\dfrac{1}{3}\right)=\dfrac{16}{7}\\ \Leftrightarrow\dfrac{19}{6}\cdot x=\dfrac{16}{7}\\ \Leftrightarrow x=\dfrac{16}{7}:\dfrac{19}{6}\\ \Leftrightarrow x=\dfrac{96}{133}\)

b) 

\(2\left[\dfrac{x-1}{40}-3\left(x-1\right)\right]=2\\ \Leftrightarrow\dfrac{x-1}{40}-3\left(x-1\right)=1\\ \Leftrightarrow\dfrac{x-1-120\left(x-1\right)}{40}=1\\ \Leftrightarrow x-1-120x+120=40\\ \Leftrightarrow-119x+119=40\\ \Leftrightarrow-119x=40-119=-79\\ \Leftrightarrow x=\dfrac{79}{119}\)

a, \(3,5x-2=\dfrac{1}{3}x+\dfrac{2}{7}\Leftrightarrow\dfrac{19}{6}x=\dfrac{2}{7}+2=\dfrac{16}{7}\Leftrightarrow x=\dfrac{16}{7}:\dfrac{19}{6}=\dfrac{96}{133}\)

b, \(2\left[x-\dfrac{1}{40}-3\left(x-1\right)\right]=2\)

\(\Leftrightarrow x-\dfrac{1}{40}-3x+3=1\Leftrightarrow-2x=1+\dfrac{1}{40}-3=-\dfrac{79}{40}\Leftrightarrow x=\dfrac{79}{80}\)

\(\left(\dfrac{1}{3}\right)^2\cdot\dfrac{1}{3}\cdot9^2\\ =\left(\dfrac{1}{3}\right)^2\cdot\dfrac{1}{3}\cdot\left(3^2\right)^2\\ =\left(\dfrac{1}{3}\right)^{1+2}\cdot3^{2\cdot2}\\ =\left(\dfrac{1}{3}\right)^3\cdot3^4\\ =\dfrac{1}{3^3}\cdot3^4\\ =\dfrac{3^4}{3^3}\\ =3\)

\(\left(\dfrac{1}{3}\right)^2.\dfrac{1}{3}.9^2=\dfrac{1}{9}.\dfrac{1}{3}.81=\dfrac{81}{27}=\dfrac{9}{3}=3\)

Ta có: 

\(-\dfrac{7}{9}=\dfrac{-14}{18}\)

\(-\dfrac{5}{6}=\dfrac{-15}{18}\)

\(\dfrac{-2}{9}=\dfrac{-4}{18}\)

\(\dfrac{4}{3}=\dfrac{24}{18}\)

\(\Rightarrow\dfrac{-15}{18}< \dfrac{-14}{18}< \dfrac{-4}{18}< 0< \dfrac{24}{18}\)

\(\Rightarrow-\dfrac{5}{6}< -\dfrac{7}{9}< -\dfrac{2}{9}< 0< \dfrac{4}{3}\)

Sắp xếp: \(\dfrac{4}{3};0;-\dfrac{2}{9};-\dfrac{7}{9};-\dfrac{5}{6}\)

\(\dfrac{2^2\cdot4\cdot32}{2^2\cdot2^5}\\ =\dfrac{2^2\cdot2^2\cdot2^5}{2^2\cdot2^5}\\ =\dfrac{2^{2+2+5}}{2^{2+5}}\\ =\dfrac{2^9}{2^7}\\ =2^{9-7}\\ =2^2\)

Lời giải:

Không mất tổng quát giả sử $m\geq n$. Ta có:

$5^m+5^n=150$

$5^n(5^{m-n}+1)=150=2.3.5^2$

Ta thấy $5^{m-n}+1$ không chia hết cho $5$ với mọi $m,n$ nguyên dương.

Do đó $5^n=5^2\Rightarrow n=2$.

$5^{m-n}+1=2.3.5^2:5^n=2.3.5^2:5^2=6$

$5^{m-2}+1=6$

$5^{m-2}=5=5^1\Rightarrow m-2=1\Rightarrow m=3$

Vậy $(m,n)=(3,2)$ và hoán vị

\(\dfrac{-5}{6}-\left(-\dfrac{7}{6}\right)+4\dfrac{1}{2}\\ =\dfrac{-5}{6}+\dfrac{7}{6}+\dfrac{9}{2}\\ =\dfrac{2}{6}+\dfrac{9}{2}\\ =\dfrac{2}{6}+\dfrac{27}{6}\\ =\dfrac{29}{6}\)

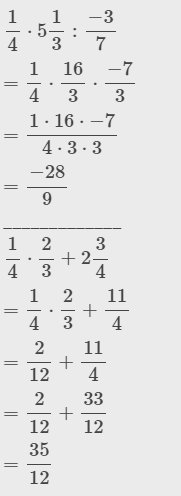
\(\dfrac{1}{4}.5\dfrac{1}{3}:\left(-\dfrac{3}{7}\right)=\dfrac{1}{4}.\dfrac{16}{3}:\left(-\dfrac{3}{7}\right)=\dfrac{4}{3}:\left(-\dfrac{3}{7}\right)=-\dfrac{28}{9}\)

\(\dfrac{1}{4}.\dfrac{2}{3}+2\dfrac{3}{4}=\dfrac{2}{12}+\dfrac{11}{4}=\dfrac{35}{12}\)

\(-\dfrac{5}{6}+\dfrac{7}{6}+4\dfrac{1}{2}=\dfrac{2}{6}+\dfrac{9}{2}=\dfrac{1}{3}+\dfrac{9}{2}=\dfrac{29}{6}\)

\(\dfrac{1}{4}\cdot5\dfrac{1}{3}:\dfrac{-3}{7}\\ =\dfrac{1}{4}\cdot\dfrac{16}{3}\cdot\dfrac{-7}{3}\\ =\dfrac{1\cdot16\cdot-7}{4\cdot3\cdot3}\\ =\dfrac{-28}{9}\)

_____________

\(\dfrac{1}{4}\cdot\dfrac{2}{3}+2\dfrac{3}{4}\\ =\dfrac{1}{4}\cdot\dfrac{2}{3}+\dfrac{11}{4}\\ =\dfrac{2}{12}+\dfrac{11}{4}\\ =\dfrac{2}{12}+\dfrac{33}{12}\\ =\dfrac{35}{12}\)

\(\dfrac{1}{4}.5\dfrac{1}{3}:\left(-\dfrac{3}{7}\right)=\dfrac{1}{4}.\dfrac{16}{3}:\left(-\dfrac{3}{7}\right)=\dfrac{4}{3}:\left(-\dfrac{3}{7}\right)=-\dfrac{28}{9}\)

\(\dfrac{1}{4}.\dfrac{2}{3}+2\dfrac{3}{4}=\dfrac{1}{6}+\dfrac{11}{4}=\dfrac{35}{12}\)

Lời giải:
Ta thấy:

$ab=\frac{3}{4}>0; bc=\frac{3}{10}>0; ca=\frac{1}{10}>0$

$\Rightarrow a,b,c>0$.

$ab=\frac{3}{4}, bc=\frac{3}{10}, ca=\frac{1}{10}$

$\Rightarrow ab.bc.ac=\frac{3}{4}.\frac{3}{10}.\frac{1}{10}$

$\Rightarrow (abc)^2=\frac{9}{400}=(\frac{3}{20})^2=(\frac{-3}{20})^2$

Do $a,b,c>0$ nên $abc>0$

$\Rightarrow abc=\frac{3}{20}$.

$a=abc:(bc)=\frac{3}{20}: \frac{3}{10}=\frac{1}{2}$

$b=abc:(ac)=\frac{3}{20}:\frac{1}{10}=\frac{3}{2}$

$c=abc:(ab)=\frac{3}{20}: \frac{3}{4}=\frac{1}{5}$

\(\dfrac{ac}{bc}=\dfrac{1}{10}:\dfrac{3}{10}=\dfrac{1}{3}\Rightarrow\dfrac{a}{b}=\dfrac{1}{3}\Rightarrow a=\dfrac{1}{3}b\)

Mà: \(ab=\dfrac{3}{4}=>\dfrac{1}{3}b\cdot b=\dfrac{3}{4}=>b^2=\dfrac{3}{4}:\dfrac{1}{3}=\dfrac{9}{4}\) 

\(\Rightarrow\left[{}\begin{matrix}b=\dfrac{3}{2}\\b=-\dfrac{3}{2}\end{matrix}\right.\)

TH1: \(b=\dfrac{3}{2}=>a=\dfrac{1}{3}\cdot\dfrac{3}{2}=\dfrac{1}{2}\)

\(\Rightarrow\dfrac{3}{2}c=\dfrac{3}{10}=>c=\dfrac{3}{10}:\dfrac{3}{2}=\dfrac{1}{5}\)

TH2: \(b=-\dfrac{3}{2}=>a=\dfrac{1}{3}\cdot\left(-\dfrac{3}{2}\right)=-\dfrac{1}{2}\)

\(\Rightarrow-\dfrac{3}{2}c=\dfrac{3}{10}=>c=\dfrac{3}{10}:-\dfrac{3}{2}=\dfrac{-1}{5}\)

\(\dfrac{-15}{20}+\left(5-\dfrac{7}{8}\right)=\dfrac{-3}{4}+5-\dfrac{7}{8}=\dfrac{-6}{8}+\dfrac{40}{8}-\dfrac{7}{8}=\dfrac{27}{8}\)

\(\dfrac{4}{-5}\cdot\left(\dfrac{2}{3}-\dfrac{7}{8}\right)=\dfrac{4}{-5}\cdot\left(\dfrac{16}{24}-\dfrac{21}{24}\right)=\dfrac{4}{-5}\cdot\dfrac{-5}{24}=\dfrac{1}{6}\)

\(\dfrac{13}{17}\cdot\dfrac{4}{5}+\dfrac{13}{17}\cdot\dfrac{-3}{4}=\dfrac{13}{17}\cdot\left(\dfrac{4}{5}+\dfrac{-3}{4}\right)=\dfrac{13}{17}\cdot\left(\dfrac{16}{20}-\dfrac{15}{20}\right)=\dfrac{13}{17}\cdot\dfrac{1}{20}=\dfrac{13}{340}\)

\(-\dfrac{15}{20}+\left(5-\dfrac{7}{8}\right)=-\dfrac{3}{4}+5-\dfrac{7}{8}=\dfrac{-6}{8}-\dfrac{7}{8}+5=-\dfrac{13}{8}+5=\dfrac{27}{8}\)

\(-\dfrac{4}{5}\left(\dfrac{2}{3}-\dfrac{7}{8}\right)=-\dfrac{4}{5}\left(-\dfrac{5}{24}\right)=\dfrac{1}{6}\)

\(\dfrac{13}{17}.\dfrac{4}{5}+\dfrac{13}{17}.\left(-\dfrac{3}{4}\right)=\dfrac{13}{17}\left(\dfrac{4}{5}-\dfrac{3}{4}\right)=\dfrac{13}{17}.\dfrac{1}{20}=\dfrac{13}{340}\)