Tứ giác MNPQ có I,K,R,S theo thứ tự là trung điểm của các cạnh MN,NP,PQ,QM. Chứng minh tứ giác IKRS là hình bình hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đây là các hẳng đẳng thức đáng nhớ. Mình chỉ cần biến đổi về dạng hằng đẳng thức rồi áp dụng.
\(x^2+2x+1=\left(x+1\right)^2\\ \left(2x-1\right)\left(2x+1\right)=4x^2-1\\ 125x^3-15y+75y^2-1=\left(5x\right)^3-3.1^2.5y+3.1.\left(5y\right)^2-1^3=\left(5y-1\right)^3\)
Các bài khác tương tự


Theo mình thì dùng phương pháp đưa về phương trình ước số sẽ dễ hơn đó bạn.
\(x^4=xy+2\) \(\Leftrightarrow x^4-xy=2\) \(\Leftrightarrow x\left(x^3-y\right)=2\)
Ta lập bảng
| \(x\) | 1 | 2 | -1 | -2 |
| \(x^3-y\) | 2 | 1 | -2 | -1 |
| \(y\) | -1 | 7 | 1 | -7 |
Do đó ta tìm được các cặp nghiệm nguyên của pt đã cho là \(\left(1;-1\right);\left(2;7\right);\left(-1;1\right);\left(-2;-7\right)\)
Hoặc dùng phương pháp rút ẩn nọ theo ẩn kia:
\(x^4=xy+2\Rightarrow y=\dfrac{x^4-2}{x}=x^3-\dfrac{2}{x}\) \(\left(x\ne0\right)\). Do \(y\inℤ\) và \(x^3\inℤ\) nên \(\dfrac{2}{x}\inℤ\) hay \(2⋮x\). Từ đó \(x\in\left\{\pm1;\pm2\right\}\). Từ đó thay vào \(y=x^3-\dfrac{2}{x}\) để tìm \(y\).
Chứ còn dùng pp kẹp thì hơi khó, để mình suy nghĩ chút :))

x4 = xy + 2
⇔ x4 - xy = 2
⇔ x(x3 - y) = 2
th1 \(\left\{{}\begin{matrix}x=2\\x^3-y=1\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=2\\y=7\end{matrix}\right.\)
th2 \(\left\{{}\begin{matrix}x=1\\x^3-y=2\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
th3 \(\left\{{}\begin{matrix}x=-2\\x^3-y=-1\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-2\\y=-7\end{matrix}\right.\)
th4 \(\left\{{}\begin{matrix}x=-1\\x^3-y=-2\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)


\(x^2+10x+25\)
\(=x^2+2.5x+5^2\)
\(=\left(x+5\right)^2\)
\(x^2-6x+9\)
\(=x^2-2.3x+3^2\)
\(=\left(x-3\right)^2\)
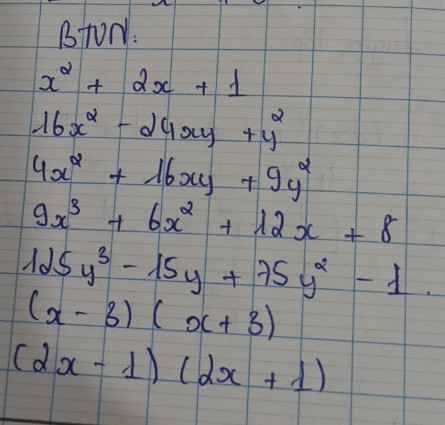
Xét tam giác MNP ta có: IK // MP; IK = 1/2 MP (IK là đường trung bình của tam giác MNP)
Xét tam giác MQP ta cũng có: RS // MP; RS = 1/2 MP
Suy ra IK // rS; IK = RS
Tương tự ta cũng chứng minh được: KR // SI; KR = SI
Tứ giác IKRS có hai cặp cạnh song song và bằng nhau, vậy tứ giác IKRS là hình bình hành