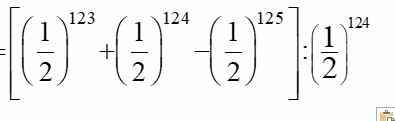
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
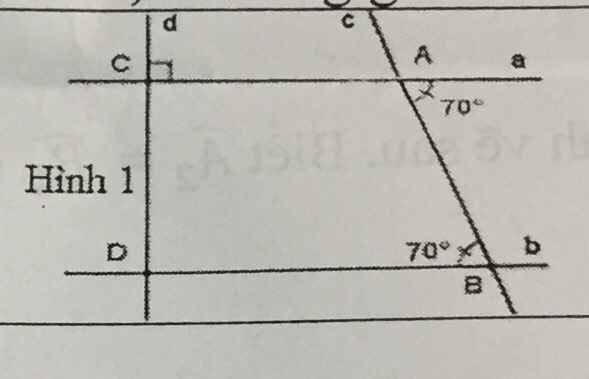
Ta thấy $\widehat{aAb}=\widehat{ABD}=70^0$. Mà 2 góc này ở vị trí so le trong nên $a\parallel b$
b.
$\widehat{CAc}=\widehat{aAb}=70^0$ (2 góc đối đỉnh)
Vì $a\parallel b, a\perp d\Rightarrow b\perp d$
$\Rightarrow \widehat{CDB}=90^0$

a) Thể tích căn phòng :
\(4,5,3,2.3,8=54,72\left(m^3\right)\)
b) Diện tích cần lăn sơn chưa trừ cửa :
\(\left(4,5+3,2\right).2+4,5.3,2=29,8\left(m^2\right)\)
Diện tích cửa :
\(25\%.\left(4,5+3,2\right).2=3,85\left(m^2\right)\)
Diện tích cần lăn sơn :
\(29,8-3,85=25,95\left(m^2\right)\)
c) Diện tích gạch của 1 hộp là :
\(4.50.50=10000\left(cm^2\right)=1\left(m^2\right)\)
Số tiền để mua gạch lót nền là :
\(4,5.3,2.150000=2160000\left(đồng\right)\)
Đáp số...

`#3107.101107`
a)
\(27< 3^x< 243\\ \Rightarrow3^3< 3^x< 3^5\\ \Rightarrow3< x< 5\\ \Rightarrow x=4\)
Vậy, `x = 4`
b)
\(2^x+2^{x+1}+2^{x+2}=56?\\ \Rightarrow2^x+2^x\cdot2+2^x\cdot4=56\\ \Rightarrow2^x\cdot\left(1+2+4\right)=56\\ \Rightarrow2^x\cdot7=56\\ \Rightarrow2^x=8\\ \Rightarrow2^x=2^3\\ \Rightarrow x=3\)
Vậy, `x = 3`
c)
\(3^x+3^{x+2}=810\\ \Rightarrow3^x+3^x\cdot9=810\\ \Rightarrow3^x\cdot\left(1+9\right)=810\\ \Rightarrow3^x\cdot10=810\\ \Rightarrow3^x=81\\ \Rightarrow3^x=3^4\\ \Rightarrow x=4\)
Vậy, `x = 4.`
a) \(27< 3^x< 243\)
\(\Rightarrow3^3< 3^x< 3^5\)
\(\Rightarrow3< x< 5\)
c) \(3^x+3^{x+2}=810\)
\(\Rightarrow3^x\left(1+3^2\right)=810\)
\(\Rightarrow3^x.10=810\)
\(\Rightarrow3^x=810:10\)
\(\Rightarrow3^x=81\)
\(\Rightarrow3^x=3^4\)
\(\Rightarrow x=4\)

`#3107.101107`
\(x^4=\dfrac{1}{81}\\ \Rightarrow x^4=\left(\dfrac{1}{3}\right)^4\\ \Rightarrow x=\dfrac{1}{3}\)
Vậy, `x =`\(\dfrac{1}{3}.\)

A=\(\dfrac{1\cdot4}{2\cdot3}\) \(\cdot\dfrac{2\cdot5}{3\cdot4}\) ...\(\dfrac{2015\cdot2018}{2016\cdot2017}\)
A=\(\dfrac{1\cdot2\cdot3\cdot...\cdot2015}{1\cdot2\cdot3\cdot...\cdot2016}\) \(\cdot\dfrac{4\cdot5\cdot...\cdot2018}{3.4\cdot...\cdot2017}\)
A=\(\dfrac{1}{2016}\) \(\cdot\dfrac{2018}{3}\) =\(\dfrac{1009}{336}\)


B = \(\left[\left(\dfrac{1}{2}\right)^{123}+\left(\dfrac{1}{2}\right)^{124}-\left(\dfrac{1}{2}\right)^{125}\right]\): \(\left(\dfrac{1}{2}\right)\)124
B = \(\left(\dfrac{1}{2}\right)\)123.\(\left(1+\dfrac{1}{2}-\dfrac{1}{4}\right)\): (\(\dfrac{1}{2}\))124
B = (\(\dfrac{1}{2}\))123. \(\dfrac{5}{4}\): (\(\dfrac{1}{2}\))124
B = (\(\dfrac{1}{2}\))124. \(\dfrac{5}{2}\) : (\(\dfrac{1}{2}\))124
B = \(\dfrac{5}{2}\)
Lời giải:
Đặt phép tính trên là $A$
$A=(\frac{1}{2})^{123}\left[1+(\frac{1}{2})-(\frac{1}{2})^2\right]: (\frac{1}{2})^{124}$
$=\left[1+\frac{1}{2}-(\frac{1}{2})^2\right]: \frac{1}{2}=\frac{5}{4}.2=\frac{5}{2}$