cho phương trình x^2-(2m+1)x+2m=0. tìm m để pt có 2 nghiệm phân biệt thỏa mãn |x1-m| - căn(x2 +(m-1)^2)=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác AHKM có \(\widehat{AHM}=\widehat{AKM}=90^0\)
nên AHKM là tứ giác nội tiếp
b: Xét (O) có
ΔMAN nội tiếp
MN là đường kính
Do đó: ΔMAN vuông tại A
Xét (O) có
\(\widehat{ABM}\) là góc nội tiếp chắn cung AM
\(\widehat{ANM}\) là góc nội tiếp chắn cung AM
Do đó: \(\widehat{ABM}=\widehat{ANM}\)
Xét ΔHBA vuông tại H và ΔANM vuông tại A có
\(\widehat{HBA}=\widehat{ANM}\)
Do đó: ΔHBA~ΔANM
c: Xét ΔHAB vuông tại H và ΔKMA vuông tại K có
\(\widehat{HAB}=\widehat{KMA}\)(ΔHBA~ΔANM)
Do đó: ΔHAB~ΔKMA
=>\(\dfrac{AH}{MK}=\dfrac{HB}{AK}\)
=>\(AH\cdot AK=MK\cdot HB\)

\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-3m\right)\)
\(=4m^2-8m+4-4m^2+12m=4m+4\)
Để phương trình có hai nghiệm phân biệt thì 4m+4>0
=>m>-1
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\left(m-1\right)=2m-2\\x_1x_2=\dfrac{c}{a}=m^2-3m\end{matrix}\right.\)
\(\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}=4\)
=>\(\dfrac{x_1^2+x_2^2}{\left(x_1x_2\right)^2}=4\)
=>\(\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{\left(x_1x_2\right)^2}=4\)
=>\(\left(2m-2\right)^2-2\left(m^2-3m\right)=4\left(m^2-3m\right)^2\)
=>\(4m^2-8m+4-2m^2+6m=4\left(m^2-3m\right)^2\)
=>\(2m^2-2m+4=4\left(m^2-3m\right)^2\)
=>\(2\left(m^4-6m^2+9\right)=m^2-m+2\)
=>\(2m^4-12m^2+18-m^2+m-2=0\)
=>\(2m^4-13m^2+m+16=0\)
=>\(m\in\left\{-2,27;-1,21;1,37;2,12\right\}\)

a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
\(\widehat{KBN}\) là góc tạo bởi tiếp tuyến BK và dây cung BN
\(\widehat{BCN}\) là góc nội tiếp chắn cung BN
Do đó: \(\widehat{KBN}=\widehat{BCN}\)
Xét ΔKBN và ΔKCB có
\(\widehat{KBN}=\widehat{KCB}\)
\(\widehat{BKN}\) chung
Do đó: ΔKBN~ΔKCB
=>\(\dfrac{KB}{KC}=\dfrac{KN}{KB}\)
=>\(KB^2=KN\cdot KC\)
b: Ta có: \(KB^2=KN\cdot KC\)
KB=KA
Do đó: \(KA^2=KN\cdot KC\)
=>\(\dfrac{KA}{KN}=\dfrac{KC}{KA}\)
Xét ΔKAC và ΔKNA có
\(\dfrac{KA}{KN}=\dfrac{KC}{KA}\)
\(\widehat{AKC}\) chung
Do đó: ΔKAC~ΔKNA
=>\(\widehat{KCA}=\widehat{KAN}\)
Xét (O) có
\(\widehat{NCA}\) là góc tạo bởi tiếp tuyến CA và dây cung CN
\(\widehat{NMC}\) là góc nội tiếp chắn cung CN
Do đó: \(\widehat{NCA}=\widehat{NMC}\)
=>\(\widehat{NMC}=\widehat{NAK}\)
=>AB//CM
Dựa vào thông tin đã được cung cấp, chúng ta có thể chứng minh như sau:
a) Chứng minh: OA vuông góc BC tại H và BK^2=KN.KC
- Ta đã biết rằng AB = AC (do hai tiếp tuyến cắt nhau), nên tam giác ABC là tam giác cân tại A.
- Vì AO là tia phân giác của góc A nên AO là đường cao của tam giác ABC.
- Do đó, ta có OA vuông góc BC tại H.
- Ta cũng biết rằng K là trung điểm của AB, nên ta có BK = KC.
- Từ đây, ta có thể chứng minh rằng (BK^2 = KN \cdot KC).
b) Chứng minh: MC//AB
- Để chứng minh MC//AB, chúng ta có thể sử dụng các tính chất của tam giác và tứ giác để chứng minh điều này. Tuy nhiên, để chứng minh chi tiết hơn, cần phải xem xét các thông tin khác về vị trí và mối quan hệ giữa các điểm trong hình học đã cho.
Tóm lại, dựa vào thông tin đã cung cấp, chúng ta có thể chứng minh a) và b) theo yêu cầu của câu hỏi.

Lời giải:
Áp dụng định lý Viet:
$x_1+x_2=5$
$x_1x_2=1$
Khi đó:
\(M=\frac{|x_1-x_2|}{\sqrt{x_1}+\sqrt{x_2}}\Rightarrow M^2=\frac{|x_1-x_2|^2}{(\sqrt{x_1}+\sqrt{x_2})^2}=\frac{x_1^2+x_2^2-2x_1x_2}{x_1+x_2+2\sqrt{x_1x_2}}\\ =\frac{(x_1+x_2)^2-4x_1x_2}{x_1+x_2+2\sqrt{x_1x_2}}=\frac{5^2-4.1}{5+2\sqrt{1}}=3\)

Lời giải:
Lấy PT(1)*2 -PT(2) thu được:
$2(x+2y)-(2x-3y)=2(m+3)-m$
$\Leftrightarrow 7y=m+6$
$\Leftrightarrow y=\frac{m+6}{7}$
$x=m+3-2y=m+3-\frac{2(m+6)}{7}=\frac{5m+9}{7}$
Vậy HPT luôn có nghiệm $(x,y)=(\frac{5m+9}{7}, \frac{m+6}{7})$
Để $x+y=-3$
$\Leftrightarrow \frac{5m+9}{7}+\frac{m+6}{7}=-3$
$\Leftrightarrow \frac{6m+15}{7}=-3$
$\Rightarrow 6m+15=-21$
$\Rightarrow m = -6$

pt thứ hai \(\Leftrightarrow\) \(y^2-\left(3x+2\right)y+2x^2+3x+1=0\) (*)
Ta có \(\Delta=\left[-\left(3x+2\right)\right]^2-4\left(2x^2+3x+1\right)\)
\(=9x^2+12x+4-8x^2-12x-4\)
\(=x^2\ge0\)
Do đó (*) có 2 nghiệm là \(\left[{}\begin{matrix}y=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{3x+2+\sqrt{x^2}}{2}=\dfrac{3x+2+\left|x\right|}{2}\\y=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{3x+2-\sqrt{x^2}}{2}=\dfrac{3x+2-\left|x\right|}{2}\end{matrix}\right.\)
Không mất tính tổng quát, giả sử \(x\ge0\). Khi đó:
\(\left[{}\begin{matrix}y=\dfrac{3x+2+x}{2}=\dfrac{4x+2}{2}=2x+1\\y=\dfrac{3x+2-x}{2}=\dfrac{2x+2}{2}=x+1\end{matrix}\right.\)
Nếu \(y=2x+1\) thì thay vào pt đầu tiên, ta có:
\(x^2+\left(2x+1\right)^2+x+2x+1=8\)
\(\Leftrightarrow5x^2+7x-6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\) \(\Rightarrow y=2x+1=2.\dfrac{3}{5}+1=\dfrac{11}{5}\)
Nếu \(y=x+1\) thì thế vào pt đầu tiên, ta có:
\(x^2+\left(x+1\right)^2+x+x+1=8\)
\(\Leftrightarrow2x^2+4x-6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-3\left(loại\right)\end{matrix}\right.\) \(\Rightarrow y=x+1=1+1=2\)
Vậy ta tìm được 2 cặp nghiệm là \(\left(\dfrac{3}{5},\dfrac{11}{5}\right)\) và \(\left(1,2\right)\)
Tương tự như vậy, xét TH \(x< 0\) thì ta tìm được thêm 2 cặp nghiệm chính là \(\left(-2,-3\right)\) và \(\left(-3,-2\right)\)

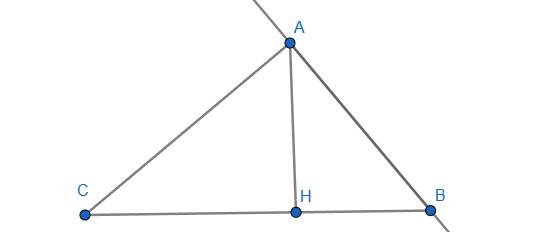
Xét tam giác ABC vuông tại A có AH là đường cao
\(BH.BC=AB^2\)
\(\Rightarrow\left(BC-HC\right)\cdot BC=AB^2\)
\(\Rightarrow\left(BC-19,2\right)\cdot BC=AB^2\)
\(\Rightarrow BC^2-19,2BC=12^2\)
\(\Rightarrow BC^2-19,2BC-144=0\)
\(\Rightarrow BC=\dfrac{48+12\sqrt{41}}{5}\approx24,96\left(cm\right)\)Xét tam giác ABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Rightarrow24,96^2=12^2+AC^2\)
\(\Rightarrow AC\approx21,89\left(cm\right)\)
Xét tam giác ABC vuông tại A có
\(S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}BC.AH\)
\(\Rightarrow\dfrac{1}{2}\cdot12\cdot21,89=\dfrac{1}{2}\cdot24,96\cdot AH\)
\(\Rightarrow AH=\dfrac{262,68}{24,96}\approx10,52\left(cm\right)\)
Vậy độ dài của và là:
Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
=>\(BH\left(BH+19,2\right)=12^2=144\)
=>\(BH^2+19,2\cdot BH-144=0\)
=>\(\left[{}\begin{matrix}BH=\dfrac{-19,2-\dfrac{24\sqrt{41}}{5}}{2}\left(loại\right)\\BH=\dfrac{-19,2+\dfrac{24\sqrt{41}}{5}}{2}=-9,6+\dfrac{12\sqrt{41}}{5}\left(nhận\right)\end{matrix}\right.\)
=>\(BH=\dfrac{-48+12\sqrt{41}}{5}\)
=>\(BC=\dfrac{-48+12\sqrt{41}}{5}+19,2=\dfrac{48+12\sqrt{41}}{5}\left(cm\right)\)
ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC=\dfrac{-48+12\sqrt{41}}{5}\cdot19,2=3,84\left(-48+12\sqrt{41}\right)\)
=>\(AH=\sqrt{3,84\left(-48+12\sqrt{41}\right)}\left(cm\right)\)
=>\(AC=\sqrt{AH^2+HC^2}=\sqrt{3,84\left(-48+12\sqrt{41}\right)+19,2^2}\)
=>\(AC=\sqrt{184,32+46,08\sqrt{41}}\)(cm)

\(\sqrt{x}+\sqrt{2-x}+\sqrt{2x-x^2}=3\) (ĐKXĐ: \(0\le x\le2\))
\(\Leftrightarrow\sqrt{x}+\sqrt{2-x}+\sqrt{x\left(2-x\right)}=3\) (1)
Đặt \(\sqrt{x}+\sqrt{2-x}=a\Rightarrow\dfrac{a^2-2}{2}=\sqrt{x\left(2-x\right)}\) (2) (a > 0)
Thay (2) vào (1), ta được:
\(a+\dfrac{a^2-2}{2}=3\)
\(\Leftrightarrow a^2+2a-2=6\)
\(\Leftrightarrow a^2+2a-8=0\) \(\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-4\end{matrix}\right.\)
Mà a > 0 nên \(a=2\)
\(\Rightarrow\sqrt{x}+\sqrt{2-x}=2\)
\(\Leftrightarrow x+2-x+2\sqrt{x\left(2-x\right)}=2\)
\(\Leftrightarrow2\sqrt{x\left(2-x\right)}=0\)
\(\Leftrightarrow x\left(2-x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(tmdk\right)\\x=2\left(tmdk\right)\end{matrix}\right.\)
Vậy ...
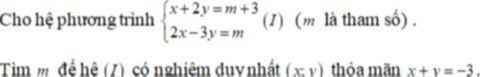
x2 -(2m+1)x+2m=0 (a=1; b = -(2m+1); c= 2m)
Δ= b2- 4ac= [-(2m+1)]2-4.1.2m= 4m2 +4m+1-8m =4m2-4m+1
= (2m-1)2
Phương trình có hai nghiệm phân biệt khi (2m-1)2>0
<=> 2m-1 >0 <=> m > 1/2
Vậy: với m>1/2 thì phương trình có hai nghiệm phân biệt
Vì với m>1/2 thì phương trình có hai nghiệm nên theo hệ thức Vi-ét, ta có:
x1+x2= -b/a= 2m+1
x1.x2= c/a = 2m
Ta có: