Giải phương trình: \(2x^4-3x^2-5=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4
a) Phương trình hoành độ giao điểm của (P) và (d):
x² = -4x - 3
⇔ x² + 4x + 3 = 0
Do a - b + c = 1 - 4 + 3 = 0 nên phương trình có hai nghiệm:
x₁ = -1; x₂ = -3
*) x₁ = -1
y = (-1)² = 1
*) x₂ = -3
y = (-3)² = 9
Vậy tọa độ giao điểm của (P) và (d) là:
(-1; 1); (-3; 9)
b) Do (d) đi qua điểm A(2; 3) nên:
2a + b = 3
⇔ b = 3 - 2a (1)
Do (d) đi qua điểm B(1; 2) nên:
a + b = 2 (2)
Thế (1) vào (2), ta có:
a + 3 - 2a = 2
⇔ -a = 2 - 3
⇔ -a = -1
⇔ a = 1
Thế a = 1 vào (1), ta có:
b = 3 - 2.1 = 1
Vậy (d): y = x + 1
Bài 8:
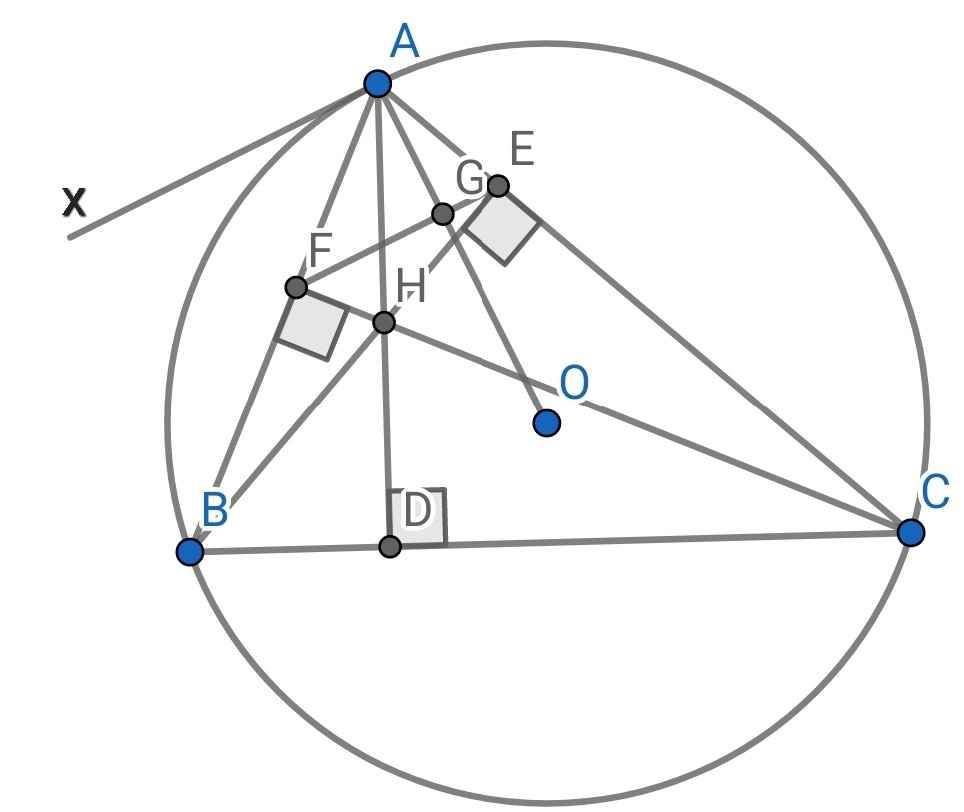
a) Xét tứ giác AEHF có:
∠HEA = ∠HFA = 90⁰ (gt)
⇒ ∠HEA + ∠HFA = 90⁰ + 90⁰ = 180⁰
⇒ AEHF nội tiếp
b) Xét tứ giác BFEC có:
∠BFC = ∠BEC = 90⁰ (gt)
⇒ F, E cùng nhìn cạnh BC dưới một góc 90⁰
⇒ BFEC nội tiếp
c) Qua A vẽ tia Ax ⊥ OA
⇒ Ax là tiếp tuyến của (O) tại A
⇒ ∠xAB = ∠ACB (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AB của (O))
Lại có:
∠ACB + ∠HBD = 90⁰ (∆EBC vuông tại E)
∠BHD + ∠HBD = 90⁰ (∆BHD vuông tại D)
⇒ ∠ACB = ∠BHD
Mà ∠BHD = ∠AHE (đối đỉnh)
⇒ ∠ACB = ∠AHE
Do AEHF nội tiếp (cmt)
⇒ ∠AHE = ∠AFE (hai góc nội tiếp cùng chắn cung AE)
⇒ ∠ACB = ∠AFE
Mà ∠ACB = ∠xAB (cmt)
⇒ ∠AFE = ∠xAB
Mà ∠AFE và ∠xAB là hai góc đồng vị
⇒ EF // Ax
Mà Ax ⊥ OA
⇒ OA ⊥ EF


Em nên gõ đề bài bằng công thức toán học biểu tượng \(\Sigma\) góc trái màn hình.

\(6x^4+7x^3+5x^2-x-2=0\)
=>\(6x^4-3x^3+10x^3-5x^2+10x^2-5x+4x-2=0\)
=>\(\left(2x-1\right)\left(3x^3+5x^2+5x+2\right)=0\)
=>\(\left(2x-1\right)\left(3x^3+2x^2+3x^2+2x+3x+2\right)=0\)
=>\(\left(2x-1\right)\left(3x+2\right)\left(x^2+x+1\right)=0\)
mà \(x^2+x+1=\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
nên (2x-1)(3x+2)=0
=>\(\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{2}{3}\end{matrix}\right.\)

ĐKXĐ: m ≠ 2
' = (-m)² - (m - 2)(m + 2)
= m² - m² + 4
= 4 > 0
Vậy phương trình luôn có hai nghiệm với mọi m ∈ R
x₁ = (m + 2)/(m - 2)
x₂ = (m - 2)/(m - 2) = 1 ∈ Z
Xét x₁ = (m + 2)/(m - 2)
= (m - 2 + 4)/(m - 2)
= 1 + 4/(m - 2)
Để x₁ ∈ Z thì 4 ⋮ (m - 2)
⇔ m - 2 ∈ Ư(4) = {-4; -2; -1; 1; 2; 4}
⇔ m ∈ {-2; 0; 1; 3; 4; 6}
Vậy m ∈ {-2; 0; 1; 3; 4; 6} thì phương trình đã cho có hai nghiệm x₁, x₂ ∈ Z


a) Do MNPQ là hình vuông (gt)
⇒ ∠QMN = 90⁰
Do NB ⊥ QA (gt)
⇒ ∠NBQ = 90⁰
Tứ giác MNBQ có:
∠QMN + ∠NBQ = 90⁰ + 90⁰ = 180⁰
⇒ MNBQ nội tiếp
b) Xét hai tam giác vuông: ∆CPN và ∆CBQ có:
∠C chung
⇒ ∆CPN ∽ ∆CBQ (g-g)
⇒ CP/CB = CN/CQ
⇒ CP.CQ = CB.CN

Lời giải:
ĐKXĐ: $x\geq 1$
PT $\Leftrightarrow \sqrt{(x-1)+8\sqrt{x-1}+16}+\sqrt{(x-1)+4\sqrt{x-1}+4}=6$
$\Leftrightarrow \sqrt{(\sqrt{x-1}+4)^2}+\sqrt{(\sqrt{x-1}+2)^2}=6$
$\Leftrightarrow |\sqrt{x-1}+4|+|\sqrt{x-1}+2|=6$
$\Leftrightarrow 2\sqrt{x-1}+6=6$
$\Leftrightarrow \sqrt{x-1}=0$
$\Leftrightarrow x-1=0$
$\Leftrightarrow x=1$ (tm)


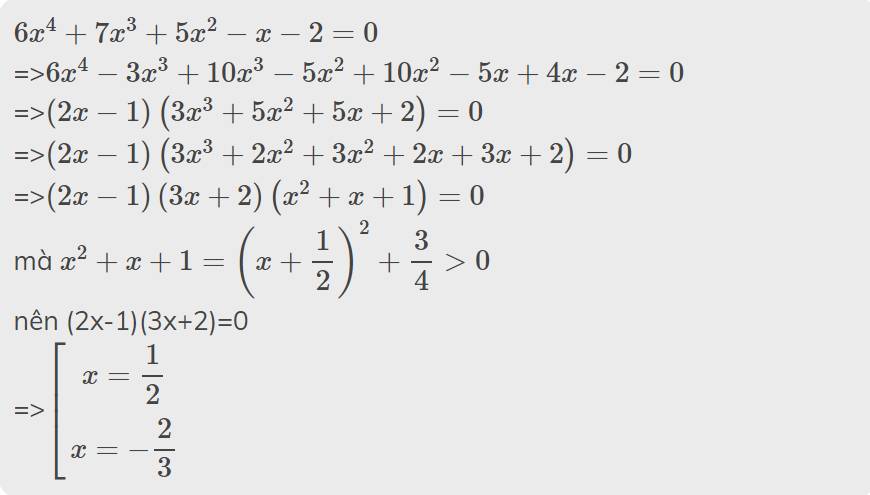
Đặt \(x^2=t\ge0\) ta được:
\(2t^2-3t-5=0\)
\(\Delta=9-4.2.\left(-5\right)=49\) nên pt có 2 nghiệm pb:
\(t_1=\dfrac{3+\sqrt{49}}{4}=\dfrac{5}{2}\) ; \(t_2=\dfrac{3-\sqrt{49}}{4}=-1< 0\) (loại)
\(\Rightarrow x^2=\dfrac{5}{2}\)
\(\Rightarrow x=\pm\dfrac{\sqrt{10}}{2}\)