
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,m=0\Leftrightarrow y=3x+2\)
Vì \(3>0\) nên hàm đồng biến
\(b,\text{Thay }x=-1;y=3\\ \Leftrightarrow-m-3+2=3\Leftrightarrow m=-4\\ c,\text{PT giao Ox: }y=0\Leftrightarrow x=-\dfrac{2}{m+3}\Leftrightarrow A\left(-\dfrac{2}{m+3};0\right)\Leftrightarrow OA=\dfrac{2}{\left|m+3\right|}\\ \text{PT giao Oy: }x=0\Leftrightarrow y=2\Leftrightarrow B\left(0;2\right)\Leftrightarrow OB=2\\ \text{Ta có }S_{OAB}=4\\ \Leftrightarrow\dfrac{1}{2}OA\cdot OB=4\Leftrightarrow\dfrac{2}{\left|m+3\right|}\cdot2=8\\ \Leftrightarrow\dfrac{4}{\left|m+3\right|}=8\\ \Leftrightarrow\left|m+3\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{5}{2}\\m=-\dfrac{7}{2}\end{matrix}\right.\)

Gọi xy là tiếp tuyến tại A của (O)
=>góc xAC=góc ABC
xy//DE
=>góc xAE=góc AED
=>góc AED=góc ABC
Xét ΔAED và ΔABC có
góc AED=góc ABC
góc EAD chung
=>ΔAED đồng dạng với ΔABC
=>AE/AB=AD/AC
=>AE*AC=AB*AD

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-20\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=8-3a=8-3\cdot7=-13\end{matrix}\right.\)

a: \(P=\left(\dfrac{2}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(=\dfrac{2\sqrt{x}+2+x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(=\dfrac{\sqrt{x}}{x-1}\)
\(P=\left(\dfrac{2}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right).\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{2\left(\sqrt{x}+1\right)+\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{x+\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{x+\sqrt{x}+2}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x-1}\)
\(\Rightarrow P=\dfrac{\sqrt{3+2\sqrt{2}}}{3+2\sqrt{2}-1}\)
\(\Rightarrow P=\dfrac{\sqrt{\left(\sqrt{2}+1\right)^2}}{2+2\sqrt{2}}\)
\(\Rightarrow P=\dfrac{\sqrt{2}+1}{2\left(\sqrt{2}+1\right)}\)
\(\Rightarrow P=\dfrac{1}{2}\)


c: \(C=\dfrac{a+\sqrt{ab}+b-\sqrt{ab}}{\sqrt{a}+\sqrt{b}}:\left(\dfrac{a}{\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}-\dfrac{b}{\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)}-\dfrac{a+b}{\sqrt{ab}}\right)\)
\(=\dfrac{a+b}{\sqrt{a}+\sqrt{b}}:\dfrac{a\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)-b\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)-\left(a+b\right)\left(a-b\right)}{\sqrt{ab}\left(a-b\right)}\)
\(=\dfrac{a+b}{\sqrt{a}+\sqrt{b}}:\dfrac{a^2-a\sqrt{ab}-b\sqrt{ab}-b^2-a^2+b^2}{\sqrt{ab}\left(a-b\right)}\)
\(=\dfrac{a+b}{\sqrt{a}+\sqrt{b}}\cdot\dfrac{\sqrt{ab}\left(a-b\right)}{-\sqrt{ab}\left(a+b\right)}\)
\(=-\left(\sqrt{a}-\sqrt{b}\right)\)

5)Áp dụng BĐT bunhia ta có:
`P^2<=(1+1+1)(x+y+y+z+z+x)`
`<=>P^2<=3.2(x+y+z)=6`
Mà `P>=0`
`=>P<=sqrt6`
Dấu "=" `<=>x=y=z=1/3`
1c của bạn đấy @@
`1c)P=A.B`
`=(sqrtx-1)/(sqrtx+3)*(sqrtx+3)/(sqrtx-3)`
`=(sqrtx-1)/(sqrtx-3)`
`|P|+P=0`
`<=>|P|=-P`
`<=>P<=0`
`<=>(sqrtx-1)/(sqrtx-3)<=0`
Vì `sqrtx-1>sqrtx-3`
`=>` $\begin{cases}\sqrt{x}-1 \ge 0\\\sqrt{x}-3 <0\end{cases}$
`<=>` $\begin{cases}\sqrt{x} \ge 1\\\sqrt{x}<3\end{cases}$
`<=>` $\begin{cases}x \ge 1\\x<9\end{cases}$
`<=>1<=x<9`
Vậy `1<=x<9` thì....

b: PTHĐGĐ là;
ax^2=2
=>ax^2-2=0
Δ=0^2-4*a*(-2)=8a
Để (P) cắt (d) tại hai điểm pb thì 8a>0
=>a>0
=>x=căn 2/a hoặc x=-căn 2/a
=>vecto OA=(căn 2/a;0); vecto OB=(-căn 2/a;0); vecto AB=(2*căn 2/a;2)
Theo đề, ta có: vecto OA*vecto OB=0 hoặc vecto OA*vecto AB=0 hoặc vecto OB*vecto AB=0
=>-2*căn 2/a+2=0 hoặc 2*căn 2/a+2=0
=>căn 2/a=1
=>a=2

b: Vì (d)//y=-2x+5/2 nên a=-2
Vậy: y=-2x+b
Phương trình hoành độ giao điểm là:
\(0.5x^2+2x-b=0\)
\(\Delta=2^2-4\cdot0.5\cdot\left(-b\right)=4+2b\)
Để (d) tiếp xúc với (P) thì 2b+4=0
hay b=-2






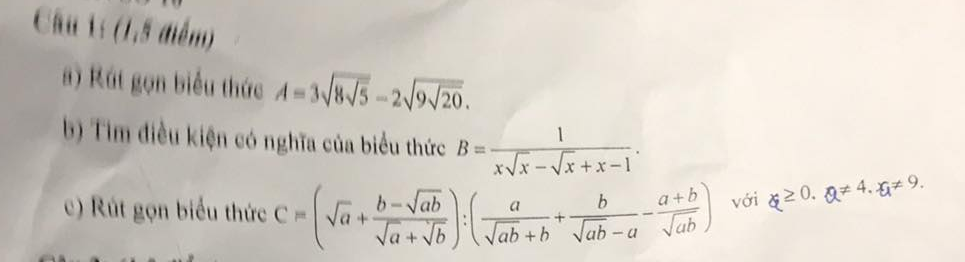


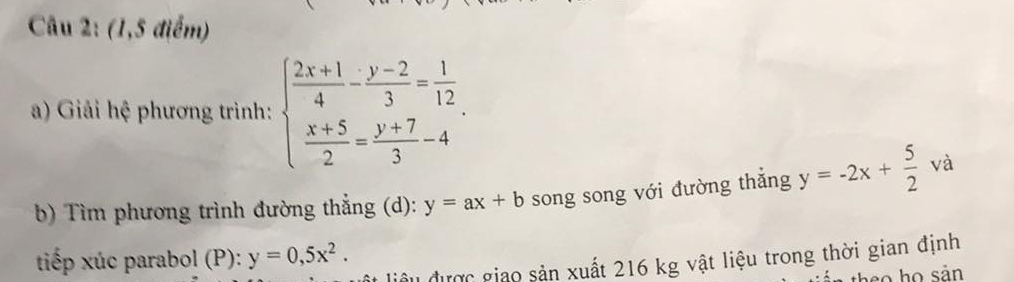
Bài 4
a) Phương trình hoành độ giao điểm của (P) và (d):
x² = -4x - 3
⇔ x² + 4x + 3 = 0
Do a - b + c = 1 - 4 + 3 = 0 nên phương trình có hai nghiệm:
x₁ = -1; x₂ = -3
*) x₁ = -1
y = (-1)² = 1
*) x₂ = -3
y = (-3)² = 9
Vậy tọa độ giao điểm của (P) và (d) là:
(-1; 1); (-3; 9)
b) Do (d) đi qua điểm A(2; 3) nên:
2a + b = 3
⇔ b = 3 - 2a (1)
Do (d) đi qua điểm B(1; 2) nên:
a + b = 2 (2)
Thế (1) vào (2), ta có:
a + 3 - 2a = 2
⇔ -a = 2 - 3
⇔ -a = -1
⇔ a = 1
Thế a = 1 vào (1), ta có:
b = 3 - 2.1 = 1
Vậy (d): y = x + 1
Bài 8:
a) Xét tứ giác AEHF có:
∠HEA = ∠HFA = 90⁰ (gt)
⇒ ∠HEA + ∠HFA = 90⁰ + 90⁰ = 180⁰
⇒ AEHF nội tiếp
b) Xét tứ giác BFEC có:
∠BFC = ∠BEC = 90⁰ (gt)
⇒ F, E cùng nhìn cạnh BC dưới một góc 90⁰
⇒ BFEC nội tiếp
c) Qua A vẽ tia Ax ⊥ OA
⇒ Ax là tiếp tuyến của (O) tại A
⇒ ∠xAB = ∠ACB (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AB của (O))
Lại có:
∠ACB + ∠HBD = 90⁰ (∆EBC vuông tại E)
∠BHD + ∠HBD = 90⁰ (∆BHD vuông tại D)
⇒ ∠ACB = ∠BHD
Mà ∠BHD = ∠AHE (đối đỉnh)
⇒ ∠ACB = ∠AHE
Do AEHF nội tiếp (cmt)
⇒ ∠AHE = ∠AFE (hai góc nội tiếp cùng chắn cung AE)
⇒ ∠ACB = ∠AFE
Mà ∠ACB = ∠xAB (cmt)
⇒ ∠AFE = ∠xAB
Mà ∠AFE và ∠xAB là hai góc đồng vị
⇒ EF // Ax
Mà Ax ⊥ OA
⇒ OA ⊥ EF