3333-2222=
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

Gọi H chân đường kẻ từ A của lăng trụ
Khi đó A'H là là hình chiếu của AA' trên mp
Xét tam giác AA'H vuông tại H có : \(SinA'=\frac{AH}{AA'}\)
\(AH=AA'.SinA'=AA'.Sin60^o=\frac{b\sqrt{3}}{2}\)
Do tam giác A'B'C' là tam giác đều nên chiều cao của tam giác : \(\frac{a\sqrt{3}}{2}\)
Thể tích ABC.A'B'C' : V = \(\frac{1}{3}\). AH . \(S_{A'B'C'}=\frac{3}{8}\)\(a^2b\)
Đáp án đó

Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn [–π2;3π2][–π2;3π2] và các hàm số y = |x| trên khoảng (-∞; +∞).

1. Định nghĩa
Hàm số mũ là hàm số có dạng y= ax, hàm số lôgarit là hàm số có dạng y = logax ( với cơ số a dương khác 1).
2. Tính chất của hàm số mũ y= ax (a>0,a≠1)(a>0,a≠1).
- Tập xác định: RR.
- Đạo hàm: ∀x∈R,y′=axlna∀x∈R,y′=axlna.
- Chiều biến thiên
+) Nếu a>1a>1 thì hàm số luôn đồng biến
+) Nếu 0<a<10<a<1 thì hàm số luôn nghịch biến
- Tiệm cận: trục Ox là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành ( y= ax > 0, ∀x), và luôn cắt trục tung tại điểm (0;1)(0;1) và đi qua điểm (1;a)(1;a).
3. Tính chất của hàm số lôgarit y = logax (a>0,a≠1)(a>0,a≠1).
- Tập xác định: (0;+∞)(0;+∞).
- Đạo hàm ∀x∈(0;+∞),y′=1xlna∀x∈(0;+∞),y′=1xlna.
- Chiều biến thiên:
+) Nếu a>1a>1 thì hàm số luôn đồng biến
+) Nếu 0<a<10<a<1 thì hàm số luôn nghịch biến
- Tiệm cận: Trục Oy là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0)(1;0) và đi qua điểm (a;1)(a;1).
4. Chú ý
- Nếu a>1a>1 thì lna>0lna>0, suy ra (ax)′>0∀x(ax)′>0∀x và (logax)’ > 0, ∀x > 0;
do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.
Tương tự, nếu 0<a<10<a<1 thì lna<0lna<0, (ax)’ < 0 và (logax)’ < 0, ∀x > 0; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.
- Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành
(ln|x|)′=1x,∀x≠0(ln|x|)′=1x,∀x≠0 và (loga|x|)’ = 1xlna1xlna, ∀x≠≠ 0.
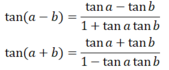
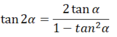
TL
= 1111
~HT~
Học dốt mà lớp 12 là 4 chữ số thôi