x = ( 6 và 3/5 :6 - 0,125 x 8 + 2 và 2/15 x 0,03 ) x 11/4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mà Ư(15)={ 3;5;15}
=> 2n+3 E {3,5,15;-3;-5,-15}
=> 2n E{0;2;12;-6-8;-18}
=> n E { 0;1;6;-3;-4;-9}
Vậy x E { 0,1,6,-3;-4,-9} E = thuộc
\(2n+3\inƯ\left(15\right)=\left\{\pm1;\pm3;\pm5;\pm15\right\}\)
\(\rightarrow2n=\left\{-4;-2;0;-6;2;-8;12;-18\right\}\)
\(\rightarrow n=\left\{-2;-1;0;-3;1;-4;6;-9\right\}\)

Bài toán này liên quan đến hình học và tính toán trên đường tròn. Để giải bài toán này, chúng ta cần sử dụng các công thức hình học cơ bản.
a) Để tính khoảng cách từ điểm O đến đường AB, ta có thể sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.
b) Để tính số đo cung nhỏ AB, ta cần sử dụng công thức tính độ dài cung trên đường tròn.
c) Để tính diện tích hình bán nguyệt giới hạn bởi dây cung AB và cung nhỏ AB, ta có thể sử dụng công thức tính diện tích hình tròn và hình tam giác.
d) Để tính IA và IB, ta có thể sử dụng định lý cosin trong tam giác vuông và các công thức hình học khác.

Trong 6 giờ đầu, trung bình mỗi giờ ô tô đi được:
\(\dfrac{40.3+50.3}{6}=45\left(km\right)\)
Quãng đường ô tô đi trong 7 giờ là :
\(\left(45+1\right).7=322\left(km\right)\)
Giờ thứ 7 ô tô cần đi là:
\(322-\left(40.3+50.3\right)=52\left(km\right)\)
Đáp số: \(52km\)
Vận tốc trung bình của ô tô trong 6 giờ đầu là:
\(\left(40\times3+50\times3\right):\left(3+3\right)=45\) (km/h)
Vận tốc trung bình của ô tô khi tăng thêm 1 km/h là:
\(45+1=46\) (km/h)
Quãng đường ô tô đi được trong 7 giờ là:
\(46\times7=322\left(km\right)\)
Quãng đường ô tô đi được trong giờ thứ 7 là:
\(322-45\times6=52\left(km\right)\)

\(\dfrac{x-1}{69}+\dfrac{x-2}{68}=\dfrac{x-5}{65}+\dfrac{x-6}{64}\)
\(\Leftrightarrow\left(\dfrac{x-1}{69}-1\right)+\left(\dfrac{x-2}{68}-1\right)-\left(\dfrac{x-5}{65}-1\right)-\left(\dfrac{x-6}{64}-1\right)=0\)
\(\Leftrightarrow\dfrac{x-70}{69}+\dfrac{x-70}{68}-\dfrac{x-70}{65}-\dfrac{x-70}{64}=0\)
\(\Leftrightarrow\left(x-70\right)\left(\dfrac{1}{69}+\dfrac{1}{68}-\dfrac{1}{65}-\dfrac{1}{64}\right)=0\)
\(\Leftrightarrow x-70=0\) (do \(\dfrac{1}{69}+\dfrac{1}{68}-\dfrac{1}{65}-\dfrac{1}{64}\ne0\))
\(\Rightarrow x=70\)

Giải:
Đổi 2 tấn 4 tạ: = 2400 kg
Tổng số xe tham gia chở cám là:
3 + 4 = 7 (xe)
Tổng số cám mà cả đoàn xe đã chở là:
2400 x 3 + 2820 x 4 = 18480 (kg)
Trung bình mỗi xe chở được số ki-lô-gam cám là:
18480 : 7 = 2640 (kg)
Đáp số:...

Giải:
Sau khi có khác lên tàu và xuồn tàu thì số khách trên tàu giảm đi là:
158 - 127 = 31 (khách)
Ban đầu tàu có số khách là:
191 + 31 = 222 (khách)
Đáp số: 222 khách

\(P=\left(-\dfrac{1}{7}\right)^0+\left(-\dfrac{1}{7}\right)^1+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2017}\)
\(\left(-\dfrac{1}{7}\right).P=\left(-\dfrac{1}{7}\right)^1+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2017}+\left(-\dfrac{1}{7}\right)^{2018}\)
\(P-\left(-\dfrac{1}{7}\right)P=\left(-\dfrac{1}{7}\right)^0-\left(-\dfrac{1}{7}\right)^{2018}\)
\(\dfrac{8}{7}P=1-\dfrac{1}{7^{2018}}\)
\(\dfrac{8}{7}P=\dfrac{7^{2018}-1}{7^{2018}}\)
\(P=\dfrac{7^{2018}-1}{8.7^{2017}}\)

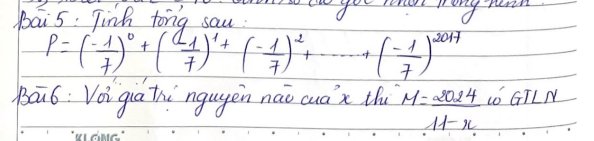
\(x=\left(6\dfrac{3}{5}:6-0,125\times8+2\dfrac{2}{15}\times0,03\right)\times\dfrac{11}{4}\)\(=\left(\dfrac{33}{5}\times\dfrac{1}{6}-\dfrac{1}{8}\times8+\dfrac{32}{15}\times\dfrac{3}{100}\right)\times\dfrac{11}{4}\\ =\left(\dfrac{11}{10}-1+\dfrac{8}{125}\right)\times\dfrac{11}{4}\\ =\dfrac{41}{250}\times\dfrac{11}{4}\\ =\dfrac{451}{1000}\)