Gọi số xe loại nhỏ được huy động là x xe (với x>2)

Số xe loại lớn là: \(x-2\) (xe)

Mỗi xe loại nhỏ có số ghế là: \(\dfrac{180}{x}\) (ghế)

Mỗi xe loại lớn có số ghế là: \(\dfrac{180}{x-2}\) (ghế)

Do mỗi xe loại nhỏ ít hơn mỗi xe loại lớn 15 ghế nên ta có pt:

\(\dfrac{180}{x-2}-\dfrac{180}{x}=15\)

\(\Rightarrow12x-12\left(x-2\right)=x\left(x-2\right)\)

\(\Leftrightarrow x^2-2x-24=0\Rightarrow\left[{}\begin{matrix}x=6\\x=-4\left(loại\right)\end{matrix}\right.\)

\(x^2\ge y^2+z^2\Rightarrow\dfrac{x^2}{y^2+z^2}\ge1\)

\(P=\dfrac{y^2+z^2}{x^2}+x^2\left(\dfrac{1}{y^2}+\dfrac{1}{z^2}\right)+2019\ge\dfrac{y^2+z^2}{x^2}+x^2.\dfrac{4}{y^2+z^2}+2019\)

\(P\ge\dfrac{y^2+z^2}{x^2}+\dfrac{x^2}{y^2+z^2}+3\dfrac{x^2}{y^2+z^2}+2019\)

\(P\ge2\sqrt{\dfrac{y^2+z^2}{x^2}.\dfrac{x^2}{y^2+z^2}}+3.1+2019=2024\)

\(P_{min}=2024\) khi \(x^2=2y^2=2z^2\)

\(ab\left(2023-\dfrac{ab}{2}\right)=\dfrac{a^4+b^4}{4}-2024\ge\dfrac{2\sqrt{a^4b^4}}{4}-2024\)

\(\Rightarrow ab\left(2023-\dfrac{ab}{2}\right)\ge\dfrac{a^2b^2}{2}-2024\)

\(\Rightarrow2023ab-\dfrac{a^2b^2}{2}\ge\dfrac{a^2b^2}{2}-2024\)

\(\Rightarrow a^2b^2-2023ab-2024\le0\)

\(\Rightarrow\left(ab+1\right)\left(ab-2024\right)\le0\)

\(\Rightarrow-1\le ab\le2024\)

\(P_{max}=2024\) khi \(a=b=\sqrt{2024}\)

\(P_{min}=-1\) khi \(\left(a;b\right)=\left(1;-1\right);\left(-1;1\right)\)

cíu

1: Phương trình hoành độ giao điểm là:

\(x^2=2\left(m+1\right)x-m-2\)

=>\(x^2-2\left(m+1\right)x+m+2=0\)

=>\(x^2-x\left(2m+2\right)+m+2=0\)

\(\text{Δ}=\left(2m+2\right)^2-4\cdot1\cdot\left(m+2\right)\)

\(=4m^2+8m+4-4m-8\)

\(=4m^2+4m-4\)

Để (P) cắt (d) tại hai điểm phân biệt thì Δ>0

=>\(4m^2+4m-4>0\)

=>\(m^2+m-1>0\)

=>\(\left[{}\begin{matrix}m>\dfrac{-1+\sqrt{5}}{2}\\m< \dfrac{-1-\sqrt{5}}{2}\end{matrix}\right.\)

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+2\\x_1x_2=\dfrac{c}{a}=m+2\end{matrix}\right.\)

\(x_1^2+2\left(m+1\right)x_2=12m+2\)

=>\(x_1^2+x_2\left(x_1+x_2\right)=12m+2\)

=>\(\left(x_1^2+x_2^2\right)+x_1x_2=12m+2\)

=>\(\left(x_1+x_2\right)^2-x_1x_2=12m+2\)

=>\(\left(2m+2\right)^2-m-2=12m+2\)

=>\(4m^2+8m+4-m-2-12m-2=0\)

=>\(4m^2-5m=0\)
=>m(4m-5)=0

=>\(\left[{}\begin{matrix}m=0\left(loại\right)\\m=\dfrac{5}{4}\left(nhận\right)\end{matrix}\right.\)

Mk đang gấp mong giúp đỡ

2.

\(\Delta'=\left(m-1\right)^2-3m\left(m-2\right)=-2m^2+4m+1>0\) (1)

Với \(m\ne0\), theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m}\\x_1x_2=\dfrac{3\left(m-2\right)}{m}\end{matrix}\right.\)

\(x_1+2x_2=1\Leftrightarrow\left(x_1+x_2\right)+x_2=1\)

\(\Leftrightarrow\dfrac{2\left(m-1\right)}{m}+x_2=1\)

\(\Leftrightarrow x_2=\dfrac{-m+2}{m}\)

Thế vào \(x_1+x_2=\dfrac{2\left(m-1\right)}{m}\Rightarrow x_1=\dfrac{2\left(m-1\right)}{m}-\dfrac{-m+2}{m}=\dfrac{3m-4}{m}\)

Thế vào \(x_1x_2=\dfrac{3\left(m-2\right)}{m}\)

\(\Rightarrow\left(\dfrac{3m-4}{m}\right)\left(\dfrac{-m+2}{m}\right)=\dfrac{3\left(m-2\right)}{m}\)

\(\Rightarrow6m^2-16m+8=0\)

\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{2}{3}\\m=2\end{matrix}\right.\)

Thế vào (1) kiểm tra thấy đều thỏa mãn

a: Xét (O) có

ΔBAC nội tiếp

BC là đường kính

Do đó: ΔBAC vuông tại A

Xét tứ giác ABDI có \(\widehat{IAB}+\widehat{IDB}=90^0+90^0=180^0\)

nên ABDI là tứ giác nội tiếp đường tròn đường kính BI

Tâm là trung điểm của BI

b: Ta có: ABDI nội tiếp

=>\(\widehat{BAD}=\widehat{BID}\)

c: Xét ΔCDI vuông tại D và ΔCAB vuông tại A có

\(\widehat{DCI}\) chung

Do đó: ΔCDI~ΔCAB

=>\(\dfrac{CD}{CA}=\dfrac{CI}{CB}\)

=>\(CD\cdot CB=CA\cdot CI\)

Tự mà làm 

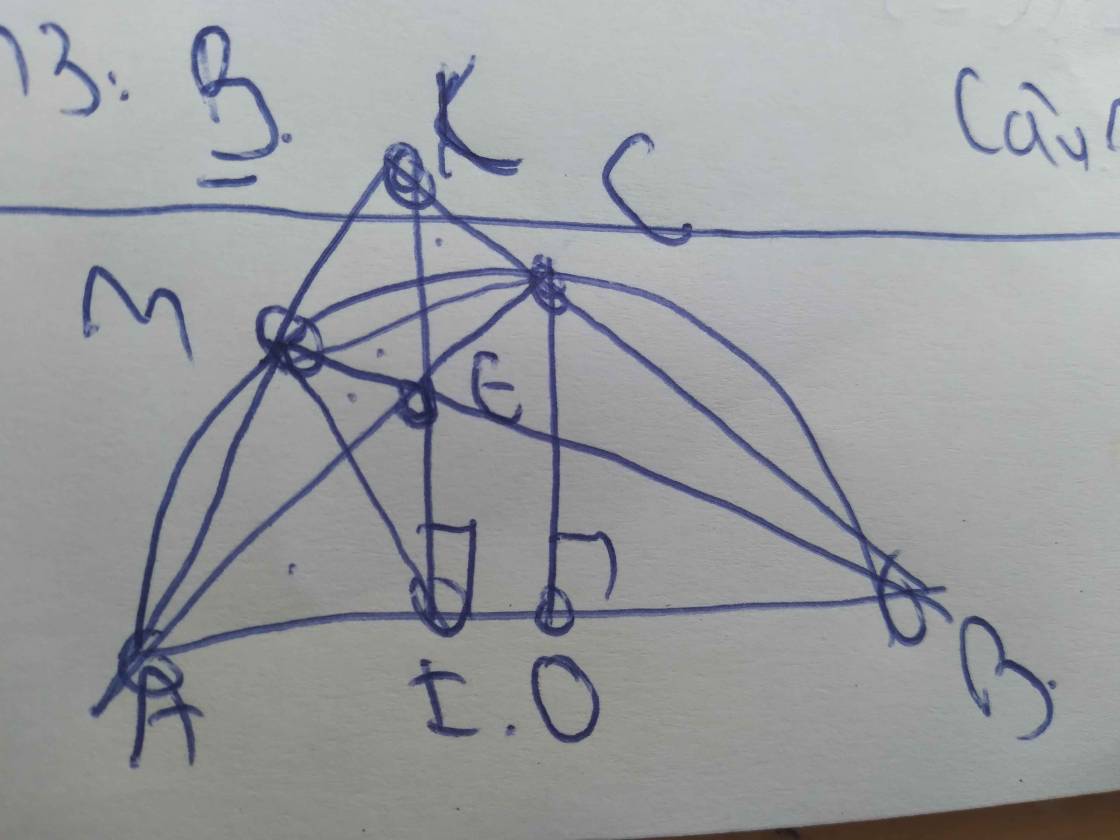
Cho đường tròn ( O: R) và đường thẳng d không có điểm chung với đường tròn.Trên d lấy một điểm M bất kì, qua M kẻ các tiếp tuyến MA, MB với đường tròn (A, B là các tiếp điểm).Kẻ cát tuyến MDE (D nằm giữa M và E, cắt bán kính OA). Gọi I là trung điểm DE...

Từ giả thiết:

\(2024abc\ge a^2+b^2+c^2\ge3\sqrt[3]{a^2b^2c^2}\Rightarrow abc\ge\dfrac{3^3}{2024^3}\)

Lại có:  

\(2024abc\ge a^2+b^2+c^2\ge\dfrac{1}{3}\left(a+b+c\right)^2\ge\dfrac{1}{3}\left(a+b+c\right).3\sqrt[3]{abc}\ge a+b+c.\sqrt[3]{\dfrac{3^3}{2024^3}}\)

\(\Rightarrow2024abc\ge\dfrac{3}{2024}\left(a+b+c\right)\)

\(\Rightarrow\dfrac{a+b+c}{abc}\le\dfrac{2024^2}{3}\)

Từ đó:

\(Q=\dfrac{a}{a^2+bc}+\dfrac{b}{b^2+ca}+\dfrac{c}{c^2+ab}\)

\(Q\le\dfrac{a}{2\sqrt{a^2.bc}}+\dfrac{b}{2\sqrt{b^2.ca}}+\dfrac{c}{2\sqrt{c^2.ab}}=\dfrac{1}{2}\left(\dfrac{1}{\sqrt{bc}}+\dfrac{1}{\sqrt{ca}}+\dfrac{1}{\sqrt{ab}}\right)\)

\(Q\le\dfrac{1}{2}\left(\dfrac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{\sqrt{abc}}\right)\le\dfrac{\sqrt{3\left(a+b+c\right)}}{2\sqrt{abc}}=\dfrac{\sqrt{3}}{2}.\sqrt{\dfrac{a+b+c}{abc}}\le\dfrac{\sqrt{3}}{2}.\sqrt{\dfrac{2024^2}{3}}=1012\)

\(Q_{max}=1012\) khi \(a=b=c=\dfrac{3}{2024}\)