a;  \(\dfrac{4}{27}\) = \(\dfrac{4\times7}{27\times7}\) = \(\dfrac{28}{189}\)

     \(\dfrac{15}{63}\) = \(\dfrac{15\times3}{63\times3}\) = \(\dfrac{45}{189}\)

     \(\dfrac{28}{189}\) < \(\dfrac{45}{189}\)

     - \(\dfrac{28}{189}\) > - \(\dfrac{45}{189}\)

Vậy - \(\dfrac{4}{27}\) > \(\dfrac{15}{-63}\) 

b;   \(\dfrac{13}{15}\) = \(\dfrac{13\times9}{15\times9}\) =  \(\dfrac{117}{135}\)

     \(\dfrac{9}{11}\) = \(\dfrac{9\times13}{11\times13}\) = \(\dfrac{117}{143}\)

     \(\dfrac{117}{135}\) > \(\dfrac{117}{143}\) 

Vậy \(\dfrac{13}{15}\) > \(\dfrac{9}{11}\) 

\(\frac{x+4}{2000}+\frac{x+3}{2001}=\frac{x+2}{2002}+\frac{x+1}{2003}\\\Leftrightarrow \frac{x+4}{2000}+\frac{x+3}{2001}-\frac{x+2}{2002}-\frac{x+1}{2003}=0\\\Leftrightarrow \left(\frac{x+4}{2000}+1\right)+\left(\frac{x+3}{2001}+1\right)-\left(\frac{x+2}{2002}+1\right)-\left(\frac{x+1}{2003}+1\right)=0\\\Leftrightarrow \frac{x+2004}{2000}+\frac{x+2004}{2001}-\frac{x+2004}{2002}-\frac{x+2004}{2003}=0\\\Leftrightarrow (x+2024)\left(\frac{1}{2000}+\frac{1}{2001}-\frac{1}{2002}-\frac{1}{2003}\right)=0\\\Leftrightarrow x+2024=0(\text{vì }\frac{1}{2000}+\frac{1}{2001}-\frac{1}{2002}-\frac{1}{2003} \ne0)\\\Leftrightarrow x=-2024\)

Vậy phương trình có 1 nghiệm duy nhất là $x=-2024$.

a: \(-\dfrac{19}{49}=\dfrac{-19\cdot47}{49\cdot47}=\dfrac{-893}{2303}\)

\(\dfrac{-23}{47}=\dfrac{-23\cdot49}{47\cdot49}=\dfrac{-1127}{2303}\)

mà -893>-1127

nên \(-\dfrac{19}{49}>-\dfrac{23}{47}\)

b: \(\dfrac{-5}{8}=\dfrac{-5\cdot5}{8\cdot5}=\dfrac{-25}{40}\)

\(\dfrac{7}{-10}=\dfrac{-7}{10}=\dfrac{-7\cdot4}{10\cdot4}=\dfrac{-28}{40}\)

mà -25>-28

nên \(-\dfrac{5}{8}>\dfrac{7}{-10}\)

c: \(\dfrac{24}{35}=\dfrac{24\cdot6}{35\cdot6}=\dfrac{144}{210};\dfrac{19}{30}=\dfrac{19\cdot7}{30\cdot7}=\dfrac{133}{210}\)

mà 144>133

nên \(\dfrac{24}{35}>\dfrac{19}{30}\)

\(-1,25=-\dfrac{125}{100}=-\dfrac{5}{4}\)

a: \(-\dfrac{15}{21}=\dfrac{-15:3}{21:3}=\dfrac{-5}{7}=\dfrac{-5\cdot11}{7\cdot11}=\dfrac{-55}{77}\)

\(\dfrac{-36}{44}=\dfrac{-36:4}{44:4}=\dfrac{-9}{11}=\dfrac{-9\cdot7}{11\cdot7}=\dfrac{-63}{77}\)

mà -55>-63

nên \(-\dfrac{15}{21}>-\dfrac{36}{44}\)

b: \(-\dfrac{16}{30}=\dfrac{-16:2}{30:2}=\dfrac{-8}{15}=\dfrac{-8\cdot4}{15\cdot4}=\dfrac{-32}{60}\)

\(\dfrac{-35}{84}=\dfrac{-35:7}{84:7}=\dfrac{-5}{12}=\dfrac{-5\cdot5}{12\cdot5}=\dfrac{-25}{60}\)

mà -32<-25

nên \(-\dfrac{16}{30}< -\dfrac{35}{84}\)

c: \(\dfrac{-5}{91}=\dfrac{-5\cdot101}{91\cdot101}=\dfrac{-505}{9191}\)

mà -505<-501

nên \(-\dfrac{5}{91}< -\dfrac{501}{9191}\)

a) Rút gọn:

\(-\dfrac{15}{21}=-\dfrac{15:3}{21:3}=-\dfrac{5}{7}\)

\(-\dfrac{36}{44}=-\dfrac{36:4}{44:4}=-\dfrac{9}{11}\)

Quy đồng(MSC:77)

\(-\dfrac{5}{7}=-\dfrac{5.11}{7.11}=-\dfrac{55}{77}\\ -\dfrac{9}{11}=-\dfrac{9.7}{11.7}=-\dfrac{63}{77}\)

Nhận thấy: \(-\dfrac{55}{77}>-\dfrac{63}{77}\Rightarrow-\dfrac{15}{21}>-\dfrac{36}{44}\)

b) Rút gọn:

\(-\dfrac{16}{30}=-\dfrac{16:2}{30:2}=-\dfrac{8}{15}\\ -\dfrac{35}{84}=-\dfrac{35:7}{84:7}=-\dfrac{5}{12}\)

Quy đồng (MSC:60)

\(-\dfrac{8}{15}=-\dfrac{8.4}{15.4}=-\dfrac{32}{60}\\ -\dfrac{5}{12}=-\dfrac{5.5}{12.5}=-\dfrac{25}{60}\)

Nhận thấy: \(-\dfrac{32}{60}< -\dfrac{25}{60}\Rightarrow-\dfrac{16}{30}< -\dfrac{35}{84}\)

c) \(-\dfrac{5}{91}=-\dfrac{5.101}{91.101}=-\dfrac{505}{9191}< -\dfrac{501}{9191}\)

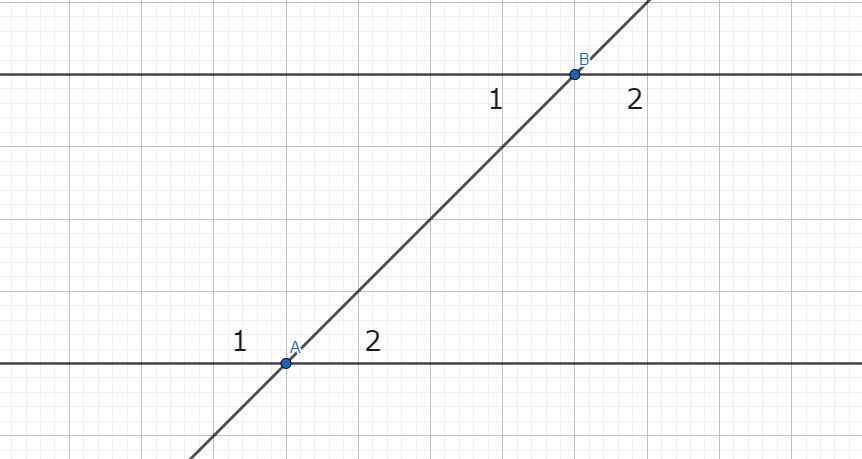 Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)

Mặt khác:

\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\) (hai cặp góc kề bù)

Mà \(\widehat{A_1}=\widehat{B_2}\) nên:

\(\widehat{A_2}=\widehat{B_1}\) Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì các cặp góc so le trong còn lại cũng bằng nhau.

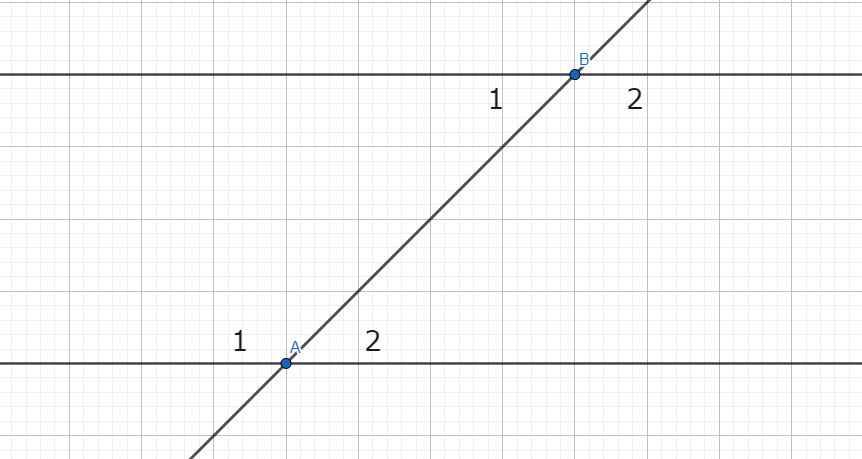Giả sử \(\widehat{A_1}\) và \(\widehat{B_2}\) là cặp góc so le trong đề bài cho.

Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)

Mặt khác:

\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)(hai cặp góc kề bù)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\)

Mà \(\widehat{A_1}=\widehat{B_2}\) nên:

\(\widehat{A_2}=\widehat{B_1}\) hay cặp góc so le trong còn lại bằng nhau

Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì cặp góc so le trong còn lại cũng bằng nhau.

1. Xét tam giác ABC vuông tại A:

• Góc B + Góc C = 90 độ (hai góc nhọn trong tam giác vuông)

2. Xét tam giác AHC vuông tại H:

• Góc CAH + Góc C = 90 độ (hai góc nhọn trong tam giác vuông)

3. Từ (1) và (2) suy ra:

• Góc B = Góc CAH

4. Gọi I là giao điểm của tia phân giác góc ABC và tia phân giác góc CAH:

• Góc ABI = Góc CBI (tính chất tia phân giác)
• Góc CAI = Góc IAH (tính chất tia phân giác)

5. Xét tam giác ABI:

• Góc ABI + Góc BAI + Góc BIA = 180 độ (tổng ba góc trong tam giác)
• Góc ABI = Góc CBI (cmt)
• Góc CAI = Góc IAH (cmt)
• Góc B = Góc CAH (cmt)

=> Góc BIA = 90 độ

6. Kết luận:

• Tia phân giác góc ABC và tia phân giác góc CAH vuông góc với nhau tại I.

Vậy, tia phân giác của góc ABC và góc CAH vuông góc với nhau.

a) Với x thuộc Z, hiển nhiên cả tử và mẫu đều nguyên

Để A là số hữu tỉ thì:

\(x-1\ne0\Rightarrow x\ne1\)

Vậy để A là số hữu tỉ thì x nguyên và x khác 1

b) Để A là số hữu tỉ dương thì A là số hữu tỉ và A dương

A là số hữu tỉ câu a đã chứng minh

Xét A dương:

\(A=\dfrac{x+1}{x-1}>0\)

=>( x+1>0 và x-1>0 ) hoặc ( x+1<0 và x-1<0 )

=> (x>-1 và x>1) hoặc (x<-1 và x<1)

=> x>1 hoặc x<-1

Kết hợp ĐK A là số hữu tỉ thì x khác 1, x nguyên

Kết luận: x>1 hoặc x<-1, x nguyên thì A là số hữu tỉ dương

hoặc x thuộc Z, x khác {1;0;-1} thì A là số hữu tỉ dương

c) Để A là số hữu tỉ âm thì A là số hữu tỉ và A âm

Xét A âm:

\(A=\dfrac{x+1}{x-1}< 0\)

=> (x+1>0 và x-1<0) hoặc (x+1<0 và x-1>0)

=> (x>-1 và x<1) hoặc (x<-1 và x>1 : Vô lí )

=> -1<x<1

Kết hợp ĐK để A là số hữu tỉ thì: x nguyên và x khác 1

Kết luận: -1<x<1, x nguyên thì A là số hữu tỉ âm

Hay x = 0 thì A là số hữu tỉ âm

d) \(A=\dfrac{x+1}{x-1}=\dfrac{x-1+2}{x-1}=1+\dfrac{2}{x-1}\left(x\in Z,x\ne1\right)\)

Để A là số nguyên thì: 2/x-1 nguyên

=> 2 chia hết cho (x-1)

=> x-1 thuộc Ư(2)={1;-1;2;-2}

Bảng giá trị:

Vậy x thuộc {2;3} thì A là số nguyên dương