Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a) bằng nhau
b) bằng nhau
c) bù nhau
2. bằng nhau; song song với nhau

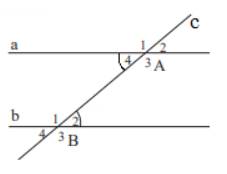
Vì đường thẳng c cắt hai đường thẳng a và b tạo thành một cặp góc so le trong ( góc A4 và B3) bằng nhau nên a // b ( Dấu hiệu nhận biết 2 đường thẳng song song)
Vì a // b nên theo tính chất của 2 đường thẳng song song:
a) Các so le trong bằng nhau
b) Các góc đồng vị bằng nhau

a) Ta có các cặp góc đồng vị là: A1 và B1; A2 và B2 ; A3 và B3 ; A4 và B4
Giả sử đã cho : A1 = B1
ta có: A1 = A3 (đối đỉnh) ; B1 = B3 (đối đỉnh) => A3 =B3
Ta có: A1 + A2 = 180o (2 góc kề bù)
B1 + B2 = 180o (2 góc kề bù)
Mà A1 = B1 nên A2 = B2
Tương tự, A2 = A4 và B2 = B4 (đối đỉnh) nên A4 = B4
b) Các cặp góc so le trong là: A2 và B4 ; A3 và B1
Theo câu a) A2 = B2 mà B2 = B4 (do đối đỉnh) nên A2 = B4
Tương tư với A3 và B1
c) các cặp góc so le ngoài là: A1 và B3 ; A4 và B2
Ta có: A1 = B1 ( giả thiết) mà B1 = B3 (do đối đỉnh) => A1 = B3
A4 và B2 : tương tự
d) Các cặp góc trong cùng phía: A2 và B1 ; A3 và B4
Ta có: A1 + A2 = 180o (do kề bù)
Mà A1 = B1 nên B1 + A2 = 180o => A2 và B1 bù nhau
A3 và B4 : tương tự
e) các cặp góc ngoài cùng phía : A1 và B2 ; A4 và B3
Ta có: B1 + B2 = 180o ( do kề bù)
Mà A1 = B1 nên A1 + B2 = 180o => A1 và B2 bù nhau
A4 và B3 : tương tự
Mặt khác:
\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\) (hai cặp góc kề bù)
Mà \(\widehat{A_1}=\widehat{B_2}\) nên:
\(\widehat{A_2}=\widehat{B_1}\) Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì các cặp góc so le trong còn lại cũng bằng nhau.
Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)
Mặt khác:
\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)(hai cặp góc kề bù)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\)
Mà \(\widehat{A_1}=\widehat{B_2}\) nên:
\(\widehat{A_2}=\widehat{B_1}\) hay cặp góc so le trong còn lại bằng nhau
Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì cặp góc so le trong còn lại cũng bằng nhau.