\(P\left(x\right)⋮x-2\)

=>\(x^4-3x^3+5x^2+ax-a⋮x-2\)

=>\(x^4-2x^3-x^3+2x^2+3x^2-6x+\left(a+6\right)x-\left(2a+12\right)+2a+12-a⋮x-2\)

=>a+12=0

=>a=-12

\(P=\left|2018-x\right|+\left|2019-x\right|\)

\(=\left|x-2018\right|+\left|2019-x\right|>=\left|x-2018+2019-x\right|=1\)

Dấu '=' xảy ra khi 2018<=x<=2019

\(4x^2-5x+a⋮2x-3\)

=>\(4x^2-6x+x-1,5+a+1,5⋮2x-3\)

=>a+1,5=0

=>a=-1,5

Nguyễn Lê Phước Thịnh 6x đâu ra vậy bạn

Đặt D(x)=0

=>\(x^2-7x+10=0\)

=>\(x^2-2x-5x+10=0\)

=>x(x-2)-5(x-2)=0

=>(x-2)(x-5)=0

=>\(\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)

a: \(P\left(x\right)=2x^2-2x^4-4x-1+x^3\)

\(=-2x^4+x^3+2x^2-4x-1\)

\(Q\left(x\right)=x^3-4x-4-3x^4\)

\(=-3x^4+x^3-4x-4\)

b: \(P\left(x\right)=-2x^4+x^3+2x^2-4x-1\)

=>Bậc là 4

\(Q\left(x\right)=-3x^4+x^3-4x-4\)

=>Bậc là 4

c: P(x)+Q(x)

\(=-2x^4+x^3+2x^2-4x-1-3x^4+x^3-4x-4\)

\(=-5x^4+2x^3+2x^2-8x-5\)

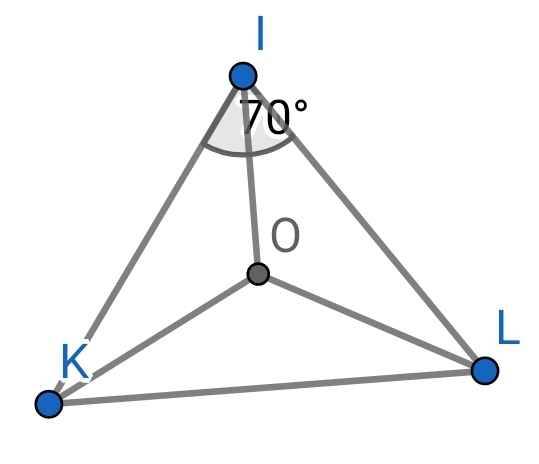
a) Do KO là tia phân giác của ∠IKL (gt)

⇒ ∠OKL = ∠OKI = ∠IKL : 2

Do LO là tia phân giác của ∠ILK (gt)

⇒ ∠ILO = ∠OLK = ∠ILK : 2

∆IKL có:

∠IKL + ∠ILK + ∠KIL = 180⁰ (tổng ba góc trong ∆IKL)

⇒ ∠IKL + ∠ILK = 180⁰ - ∠KIL

= 180⁰ - 70⁰

= 110⁰

⇒ ∠OKL + ∠OLK = ∠IKL : 2 + ∠ILK : 2

= (∠IKL + ∠ILK) : 2

= 110⁰ : 2

= 55⁰

∆OKL có:

∠OKL + ∠OLK + ∠KOL = 180⁰ (tổng ba góc trong ∆OKL)

⇒ ∠KOL = 180⁰ - (∠OKL + ∠OLK)

= 180⁰ - 55⁰

= 125⁰

b) Do KO và LO là hai đường phân giác của ∆KIL (gt)

⇒ IO là đường phân giác thứ ba của ∆KIL

⇒ IO là tia phân giác của ∠KIL

⇒ ∠KIO = ∠KIL : 2

= 70⁰ : 2

= 35⁰

c) Do O là giao điểm của ba đường phân giác của ∆KIL

⇒ O cách đều ba cạnh của ∆KIL

cảm ơn

Chiều rộng hình chữ nhật là:

\(18:2=9\left(m\right)\)

Chiều dài hình chữ nhật:

\(9+3=12\left(m\right)\)

Ta gọi a là chiều rộng.

Ta có:

(a + 3) x a = S

(a + 3 + 2) x a = S + 18

(a + 5) x a = S + 18

(a + 5) x a - (a + 3) x a = S + 18 - S

2a = 18

  a = 18 : 2

  a = 9

⇒ Chiều rộng của hình chữ nhật là: 9 cm

⇒ Chiều dài của hình chữ nhật là: 9 + 3 = 12 (cm)

Đáp số: Chiều rộng: 9 cm

             Chiều dài: 12 cm

Lời giải:

$\frac{a}{b}< \frac{c}{d}\Rightarrow \frac{ad-bc}{bd}<0$

$\Rightarrow ad-bc<0$ (do $b,d>0$)

$\Rightarrow bd> ad$

Khi đó:

$\frac{a+c}{b+d}-\frac{a}{b}=\frac{bc-ad}{b(b+d)}>0$ do $bc>ad$ và $b(b+d)>0$ với mọi $b,d>0$

$\Rightarrow \frac{a+c}{b+d}> \frac{a}{b}$

Mặt khác:

\(\frac{a+c}{b+d}-\frac{c}{d}=\frac{ad-bc}{d(b+d)}<0\) do $ad< bc$ và $d(b+d)>0$ với $b,d>0$

$\Rightarrow \frac{a+c}{b+d}< \frac{c}{d}$

Vậy ta có đpcm.