
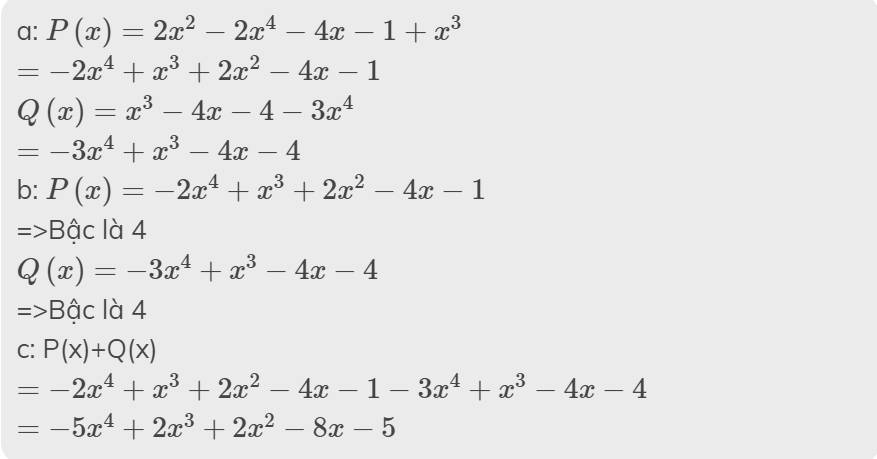
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

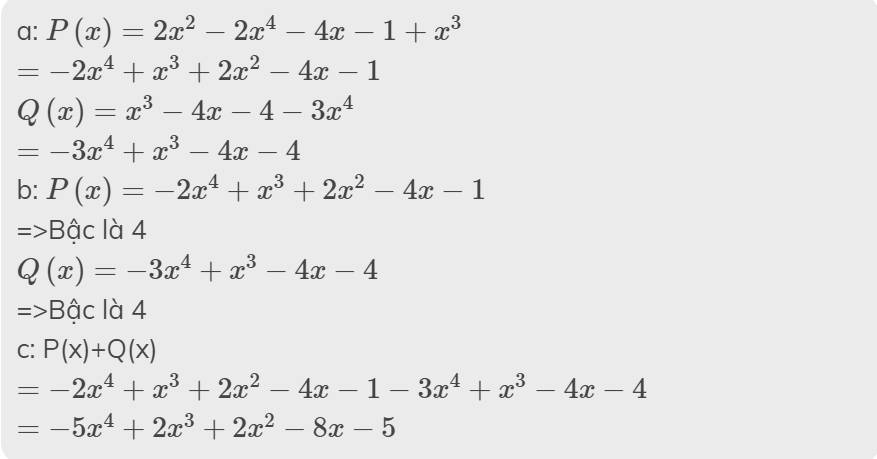

Thu gọn và sắp xếp:
P(x) = x² + 5x^4 - 3x³ + x² + 4x^4 + 3x³ - x + 5
= (5x^4 + 4x^4) + (- 3x³+ 3x³) + (x² + x²) - x + 5
= 9x^4 + 2x² - x +5
Q(x)= x - 5x³ - x² - x^4 + 4x³ - x² - 3x - 1
= -x^4 + (- 5x³ + 4x³) + (- x² - x²) + (x - 3x) - 1
= -x^4 - x³ -2x² - 2x - 1
mik mới chỉ làm đc vz thui ak
a, Ta có : \(P\left(x\right)=x^2+5x^4-3x^3+x^2+4x^4+3x^3-x+5\)
\(=2x^2+9x^4-x+5\)
\(Q\left(x\right)=x-5x^3-x^2-x^4+4x^3-x^2+3x-1\)
\(=4x-x^3-2x^2-1-x^4\)
Sắp xếp :
\(P\left(x\right)=9x^4+2x^2-x+5\)
\(Q\left(x\right)=-x^4-x^3-2x^2+4x-1\)
b, \(M\left(x\right)=9x^4+2x^2-x+5-x^4-x^3-2x^2+4x-1\)
\(=8x^4+3x+4\)Bậc : 4
c, \(N\left(x\right)=18x^4+4x^2-2x+10+x^4+x^3+2x^2-4x+1\)
\(=19x^4+6x^2-6x+11\)

a: \(P\left(x\right)=5x^5-4x^4-2x^3+4x^2+3x+6\)
Bậc là 5
\(Q\left(x\right)=-5x^5+4x^4+2x^3-4x^2+7x+\dfrac{1}{4}\)
Bậc là 5
b: H(x)=P(x)+Q(x)
\(=5x^5-4x^4-2x^3+4x^2+3x+6-5x^5+4x^4+2x^3-4x^2+7x+\dfrac{1}{4}\)
=10x+6,25
c: Để H(x)=0 thì 10x+6,25=0
hay x=-0,625

a: \(P\left(x\right)=5x^5-4x^4+2x^2+3x+6\)
\(Q\left(x\right)=-x^5+2x^4-2x^3+3x^2+x+\dfrac{1}{4}\)
b: \(P\left(x\right)+Q\left(x\right)=4x^5-2x^4-2x^3+5x^2+4x+\dfrac{25}{4}\)

a: \(Q\left(x\right)=-5x^6+2x^4+4x^3-4x-1\)
b: \(Q\left(x\right)=-5x^6+2x^4+4x^3-4x-1\)

`a)`
\(P\left(x\right)=4x+3x^2+x^2+1-5x-2x\\ =\left(3x^2+x^2\right)+\left(4x-5x-2x\right)+1\\ =4x^2-3x+1\\ Q\left(x\right)=3x+x+7-5x^2+5x-11\\ =-5x^2+\left(3x+x+5x\right)+\left(7-11\right)\\ =-5x^2+9x-4\)
`b)`
Đa thức `P(x)` có :
Bậc `2`
Đa thức `Q(x)` có :
Bậc `2`
`c)`
\(P\left(x\right)+Q\left(x\right)=\left(4x^2-3x+1\right)+\left(-5x^2+9x-4\right)\\ =4x^2-3x+1-6x^2+9x-4\\ =\left(4x^2-5x^2\right)-\left(3x-9x\right)+\left(1-4\right)\\ =-x^2+6x-3\)
a: P(x)=4x^2+4x+1-7x=4x^2-3x+1
Q(x)=-5x^2+9x-4
b: P(x) có bậc 2
Q(x) có bậc 2
c: P(x)+Q(x)=4x^2-3x+1-5x^2+9x-4=-x^2+6x-3

Để thu gọn và sắp xếp các hạng tử của mỗi đa thức, ta cần thực hiện các bước sau:
Đối với đa thức P(x): P(x) = (4x + 1 - x^2 + 2x^3) - (x^4 + 3x - x^3 - 2x^2 - 5) = 4x + 1 - x^2 + 2x^3 - x^4 - 3x + x^3 + 2x^2 + 5 = -x^4 + 3x^3 + x^2 + x + 6
Đối với đa thức Q(x): Q(x) = 3x^4 + 2x^5 - 3x - 5x^4 - x^5 + x + 2x^5 - 1 = 2x^5 - x^5 + 3x^4 - 5x^4 + x - 3x - 1 = x^5 - 2x^4 - 2x - 1
Sau khi thu gọn và sắp xếp các hạng tử, ta có: P(x) = -x^4 + 3x^3 + x^2 + x + 6 Q(x) = x^5 - 2x^4 - 2x - 1
a: \(P\left(x\right)=\left(4x+1-x^2+2x^3\right)-\left(x^4+3x-x^3-2x^2-5\right)\)
\(=4x+1-x^2+2x^3-x^4-3x+x^3+2x^2+5\)
\(=-x^4+3x^3+x^2+x+6\)
\(Q\left(x\right)=3x^4+2x^5-3x-5x^4-x^5+x+2x^5-1\)
\(=\left(2x^5-x^5+2x^5\right)+\left(3x^4-5x^4\right)+\left(-3x+x\right)-1\)
\(=-x^5-2x^4-2x-1\)
b: Bạn ghi lại đề đi bạn

a) \(...=P\left(x\right)=2x^4-x^4+3x^3+4x^2-3x^2+3x-x+3\)
\(P\left(x\right)=x^4+3x^3+x^2+2x+3\)
\(...=Q\left(x\right)=x^4+x^3+3x^2-x^2+4x+4-2\)
\(Q\left(x\right)=x^4+x^3+2x^2+4x+2\)
b) \(P\left(x\right)+Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)+\left(x^4+x^3+2x^2+4x+2\right)\)
\(\Rightarrow P\left(x\right)+Q\left(x\right)=2x^4+4x^3+3x^2+6x+5\)
\(P\left(x\right)-Q\left(x\right)=\left(x^4+3x^3+x^2+2x+3\right)-\left(x^4+x^3+2x^2+4x+2\right)\)
\(\)\(\Rightarrow P\left(x\right)-Q\left(x\right)=x^4+3x^3+x^2+2x+3-x^4-x^3-2x^2-4x-2\)
\(\Rightarrow P\left(x\right)-Q\left(x\right)=2x^3-x^2-2x+1\)

a: \(P\left(x\right)=x-2x^2+3x^5+x^4+x-1\)
\(=3x^5+x^4-2x^2+2x-1\)
\(Q\left(x\right)=3-2x-2x^2+x^4-3x^5-x^4+4x^2\)
\(=-3x^5+2x^2-2x+3\)
b: P(x)+Q(x)
\(=3x^5+x^4-2x^2+2x-1-3x^5+2x^2-2x+3\)
\(=x^4+2\)
P(x)-Q(x)
\(=3x^5+x^4-2x^2+2x-1+3x^5-2x^2+2x-3\)
\(=6x^5+x^4-4x^2+4x-4\)

a) \(P\left(x\right)=2x^3-2x+x^2-x^3+3x+2\)\(=\left(2x^3-x^3\right)+x^2+\left(3x-2x\right)+2=x^3+x^2+x+2\)
\(Q\left(x\right)=4x^3-5x^2+3x-4x-3x^3+4x^2+1\)
Q(x) \(=\left(4x^3-3x^3\right)+\left(4x^2-5x^2\right)+\left(3x-4x\right)+1\)\(=x^3-x^2-x+1\)
b) \(P\left(x\right)+Q\left(x\right)=2x^3+3\); \(P\left(x\right)-Q\left(x\right)=2x^2+2x+1\)
a) Sắp xếp theo lũy thừa giảm dần
P(x)=x^5−3x^2+7x^4−9x^3+x^2−1/4x
=x^5+7x^4−9x^3−3x^2+x^2−1/4x
=x^5+7x^4−9x^3−2x^2−1/4x
Q(x)=5x^4−x^5+x^2−2x^3+3x^2−1/4
=−x^5+5x^4−2x^3+x^2+3x^2−1/4
=−x^5+5x^4−2x^3+4x^2−1/4
b)
P(x)+Q(x)
=(x^5+7x^4−9x^3−2x^2−1/4^x)+(−x^5+5x^4−2x^3+4x^2−1/4)
=x^5+7x^4−9x^3−2x^2−1/4x−x^5+5x^4−2x^3+4x^2−1/4
=(x^5−x^5)+(7x^4+5x^4)+(−9x^3−2x^3)+(−2x^2+4x^2)−1/4x−1/4
=12x^4−11x^3+2x^2−1/4x−1/4
P(x)−Q(x)
=(x^5+7x^4−9x^3−2x^2−1/4x)−(−x^5+5x^4−2x^3+4x^2−1/4)
=x^5+7x^4−9x^3−2x^2−1/4x+x^5−5x^4+2x^3−4x^2+1/4
=(x^5+x^5)+(7x^4−5x^4)+(−9x^3+2x^3)+(−2x^2−4x^2)−1/4x+1/4
=2x5+2x4−7x3−6x2−1/4x−1/4
c) Ta có
P(0)=0^5+7.0^4−9.0^3−2.0^2−1/4.0
⇒x=0là nghiệm của P(x).
Q(0)=−0^5+5.0^4−2.0^3+4.0^2−1/4=−1/4≠0
⇒x=0không phải là nghiệm của Q(x).