đáp án E=MC ²

Công thức E=mc2E = mc^2E=mc2 là phương trình nổi tiếng của nhà vật lý học Albert Einstein. Phương trình này là một phần của thuyết tương đối hẹp và diễn tả mối quan hệ giữa năng lượng (E), khối lượng (m), và tốc độ ánh sáng trong chân không (c). Cụ thể:

• $E$ là năng lượng.
• $m$ là khối lượng.
• $c$ là tốc độ ánh sáng trong chân không, xấp xỉ 3×1083 \times 10^83×108 mét/giây.

Phương trình này cho thấy rằng khối lượng và năng lượng có thể hoán đổi cho nhau, nghĩa là một vật có khối lượng nhỏ cũng có thể chứa một lượng năng lượng khổng lồ. Điều này đã có những ứng dụng quan trọng trong nhiều lĩnh vực của vật lý, bao gồm cả việc giải thích năng lượng giải phóng trong phản ứng hạt nhân.

Albert Einstein đã công bố thuyết tương đối hẹp vào năm 1905 trong bài báo mang tên "Zur Elektrodynamik bewegter Körper" (Về điện động lực học của các vật chuyển động). Phương trình nổi tiếng E=mc2E = mc^2E=mc2 xuất hiện trong một bài báo tiếp theo vào năm 1905 với tiêu đề "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?" (Sự quán tính của một vật có phụ thuộc vào năng lượng của nó không?).

a: 

b: 

c: Tổng trị giá xuất khẩu của nước ta trong quý I giai đoạn 2020-2022 là:

63,4+78,56+89,1=231,06(tỉ USD)

d: Tổng trị giá nhập khẩu của nước ta trong quý I giai đoạn 2020-2022 là:

59,59+76,1+87,64=223,33(tỉ USD)

e: Trị giá xuất khẩu trong quý I/2020 so với quý I/2021 thì giảm:

\(\dfrac{78,56-63,4}{63,4}\simeq23,91\%\)

f: Trị giá nhập khẩu trong quý I/2021 so với quý I/2020 thì tăng:

\(\dfrac{76,1-59,59}{59,59}-100\%\simeq27.71\%\)

a) 

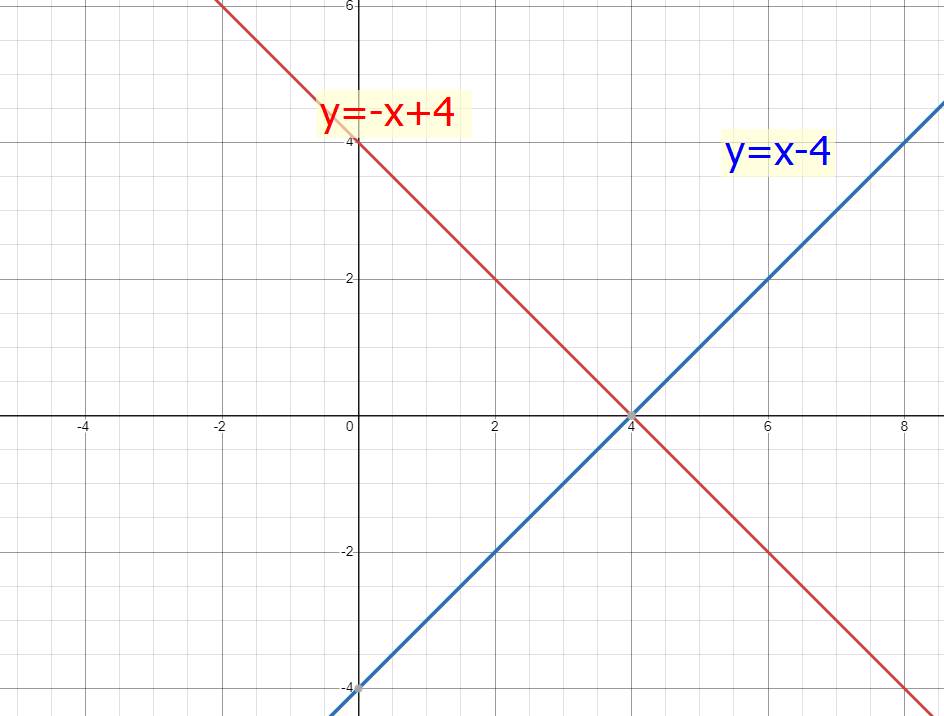
b) Hàm số y=-x+4 cắt Oy tại \(\left(0;4\right)\) \(\Rightarrow A\left(0;4\right)\)

Hàm số y=x-4 cắt Oy tại \(\left(0;-4\right)\) \(\Rightarrow B\left(0;-4\right)\)

Ta có pt hoành độ giao điểm của y=-x+4 và y=x-4 là:

\(-x+4=x-4\Leftrightarrow x=4\)

\(\Rightarrow y=4-4=0\)

\(\Rightarrow C\left(4;0\right)\)

c) Ta có: \(A\left(0;4\right)\Rightarrow OA=4\) 

\(B\left(0;-4\right)\Rightarrow OB=4\)

\(C\left(0;4\right)\Rightarrow OC=4\)

BC = OA + OB = 4 + 4 = 8 

\(\Rightarrow S_{ABC}=\dfrac{1}{2}\cdot4\cdot8=16\) (đvdt) 

a: Xác suất thực nghiệm của biến cố "Thẻ lấy ra ghi số 7" là:

\(\dfrac{6}{30}=\dfrac{1}{5}\)

b: Gọi A là biến cố "Thẻ rút ra là số nguyên tố"

=>A={2;3;5;7;11;13}

=>n(A)=6

=>\(P_A=\dfrac{6}{15}=\dfrac{2}{5}\)

=>Khi số lần rút thẻ ngày càng lớn thì xác suất thực nghiệm của biến cố A ngày càng gần với 2/5

\(\dfrac{890}{100}=\dfrac{89}{10}=8,9\)

\(\dfrac{900}{1000}=\dfrac{9}{10}=0,9\)

1235/1000000

12345/1000

132/10

109/1000

100/100

B là tập hợp của các số lẻ từ 7 đến 86

=>B={7;9;11;13;15;17;19;21;23;...;85}

Số thứ 10 từ trái qua là 25

               Giải

Các số tự nhiên lẻ từ 7 đến 86 là các số tự nhiên thuộc dãy số sau:

       7; 9; 11; 13; 15;...; 85

Dãy số trên là dãy số cách đều với khoảng cách là:

           9 - 7  = 2

Số thứ 10 của dãy số trên là: 2 x (10 - 1) + 7  = 25

Từ những lập luận trên ta có kết luận: 

 B = {7; 9; 11; 13; 15;...; 85}

Tính từ trái qua phải phần tử thứ 10 của tập B là 25.

\(A=\left(-7\right)+\left(x+1\right)^2\)

Nhận xét: \(\left(x+1\right)^2\ge0\)

\(\Rightarrow\left(-7\right)+\left(x+1\right)^2\ge-7\)

hay \(A\ge-7\) 

Dấu "=" xảy ra khi:

\(x+1=0\)

\(\Rightarrow x=-1\)

Vậy...

\(B=\left(x-2\right)^2-17\)

Nhận xét: \(\left(x-2\right)^2\ge0\)

\(\Rightarrow\left(x-2\right)^2-17\ge-17\)

hay \(A\ge-17\)

Dấu "=" xảy ra khi:

\(x-2=0\)

\(\Rightarrow x=2\)

Vậy...

Bài 3:

a: 2,9<x<3,5

mà x là số tự nhiên

nên x=3

b: 3,25<x<5,05

mà x là số tự nhiên

nên \(x\in\left\{4;5\right\}\)

c: x<3,008

mà x là số tự nhiên

nên \(x\in\left\{0;1;2;3\right\}\)

Bài 4:

a: 8<x<9

mà x là số thập phân có 1 chữ số ở phần thập phân

nên \(x\in\left\{8,1;8,2;...;8,9\right\}\)

b: 0,1<x<0,2

mà x là số thập phân có 2 chữ số ở phần thập phân

nên \(x\in\left\{0,11;0,12;...;0,19\right\}\)

c: x<19,54<y

mà x,y là hai số tự nhiên liên tiếp

nên x=19; y=20

Bài 1: Tính nhanh

a; 15,8 + 6,79 + 4,2

= (15,8 + 4,2) + 6,79

= 20 + 6,79

= 26,79

b; 18,3 - 13,4 - 4,6

= 18,3 - (13,4 + 4,6)

= 18,3 - 18

= 0,3

f; 37,6 + 2,19 + 7,81 + 2,4

= (37,6 + 2,4) + (2,19 + 7,81)

= 40 + 10

= 50

g; 118,67 - (18,17 + 40,5)

= 118,67 - 18,17 - 40,5

= 100,5 - 40,5

= 60 

\(\left\{{}\begin{matrix}\left(x-1\right)\left(2y+1\right)=\left(x-3\right)\left(y-5\right)+xy\\\left(x+1\right)\left(y+1\right)=\left(2x-1\right)\left(y+1\right)-xy\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2xy+x-2y-1=xy-5x-3y+15+xy\\xy+x+y+1=2xy+2x-y-1-xy\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x-2y-1=-5x-3y+15\\x+y+1=2x-y-1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}6x+y=16\\-x+2y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12x+2y=32\\-x+2y=-2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}13x=34\\6x+y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{34}{13}\\y=16-6x=16-6\cdot\dfrac{34}{13}=\dfrac{4}{13}\end{matrix}\right.\)