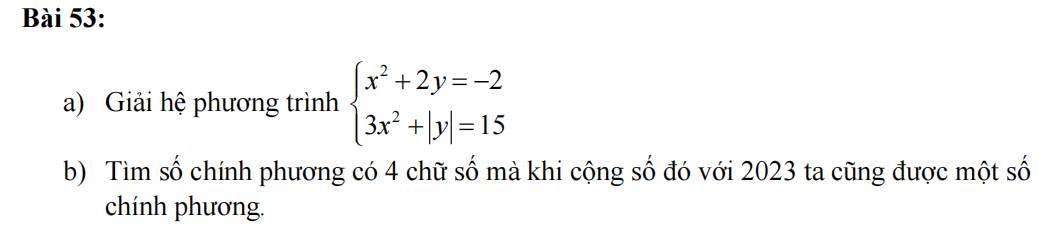Tìm số tự nhiên \(n\) \(\left(20349< n< 47238\right)\) và \(A\) để \(A=4789655-27n\) là lập phương của một số tự nhiên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(U_n=\dfrac{\left(n^2-1\right)}{n\left(n+2\right)}U_{n-1}\Rightarrow n\left(n+2\right).U_n=\left(n-1\right)\left(n+1\right).U_{n-1}\)
Đặt \(n\left(n+2\right).U_n=V_n\Rightarrow V_{n-1}=\left(n-1\right)\left(n+2-1\right).U_{n-1}=\left(n-1\right).\left(n+1\right)U_{n-1}\)
\(\Rightarrow V_n=V_{n-1}\)
\(\Rightarrow V_n=V_{n-1}=V_{n-2}=...=V_1\)
Có \(V_1=1.\left(1+2\right).U_1=1\)
\(\Rightarrow V_n=1\)
\(\Rightarrow U_n=\dfrac{V_n}{n\left(n+2\right)}=\dfrac{1}{n\left(n+2\right)}\)
\(\Rightarrow A=\dfrac{1}{1.3}+\dfrac{1}{2.4}+\dfrac{1}{3.5}+...+\dfrac{1}{2015.2017}\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2015}-\dfrac{1}{2017}\right)\)
\(=\dfrac{1}{2}\left(1+\dfrac{1}{2}-\dfrac{1}{2016}-\dfrac{1}{2017}\right)\)
\(=...\)

\(f\left(x\right)=6x^3-7x^2-16x+m\)
Do \(f\left(x\right)\) chia hết \(2x-5\), theo định lý Bezout:
\(f\left(\dfrac{5}{2}\right)=0\Rightarrow6.\left(\dfrac{5}{2}\right)^3-7.\left(\dfrac{5}{2}\right)^2-16.\left(\dfrac{5}{2}\right)+m=0\)
\(\Rightarrow m=-10\)
Khi đó \(f\left(x\right)=6x^3-7x^2-16x-10\)
Số dư phép chia cho \(3x-2\):
\(f\left(\dfrac{2}{3}\right)=6.\left(\dfrac{2}{3}\right)^3-7.\left(\dfrac{2}{3}\right)^2-16.\left(\dfrac{2}{3}\right)-10=-22\)
Do chia hết , theo định lý Bezout:
Khi đó
Số dư phép chia cho :

Lời giải:
\(\frac{1719}{3976}=\frac{1}{2+\frac{538}{1719}}=\frac{1}{2+\frac{1}{3+\frac{105}{538}}}=\frac{1}{2+\frac{1}{3+\frac{1}{5+\frac{13}{105}}}}=\frac{1}{2+\frac{1}{3+\frac{1}{5+\frac{1}{8+\frac{1}{13}}}}}\)
$\Rightarrow a=8; b=13$
\(\dfrac{1719}{3976}=\dfrac{1}{\dfrac{3976}{1719}}=\dfrac{1}{2+\dfrac{538}{1719}}=\dfrac{1}{2+\dfrac{1}{\dfrac{1719}{538}}}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{105}{538}}}\)
\(=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{\dfrac{538}{105}}}}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5+\dfrac{13}{105}}}}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5+\dfrac{1}{\dfrac{105}{13}}}}}\)
\(=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{5+\dfrac{1}{8+\dfrac{1}{13}}}}}\)

ĐKXĐ: \(0< x< 4\)
Đặt \(\left\{{}\begin{matrix}\sqrt{2+\sqrt{x}}=a>0\\\sqrt{2-\sqrt{x}}=b\ge0\end{matrix}\right.\) \(\Rightarrow a^2+b^2=4\)
\(\Rightarrow\dfrac{a^2}{\sqrt{2}+a}+\dfrac{b^2}{\sqrt{2}-b}=\sqrt{2}\)
\(\Rightarrow a^2\sqrt{2}-a^2b+ab^2+b^2\sqrt{2}=2\sqrt{2}-2b+2a-ab\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}\left(a^2+b^2\right)-ab\left(a-b\right)=2\sqrt{2}+2\left(a-b\right)-ab\sqrt{2}\)
\(\Leftrightarrow2\sqrt{2}+ab\sqrt{2}-ab\left(a-b\right)-2\left(a-b\right)=0\)
\(\Leftrightarrow\sqrt{2}\left(ab+2\right)-\left(a-b\right)\left(ab+2\right)=0\)
\(\Leftrightarrow\left(\sqrt{2}-a+b\right)\left(ab+2\right)=0\)
\(\Leftrightarrow\sqrt{2}-a+b=0\) (do \(ab\ge0\Rightarrow ab+2>0\))
\(\Leftrightarrow\sqrt{2+\sqrt{x}}-\sqrt{2-\sqrt{x}}=\sqrt{2}\)
Hiển nhiên \(2+\sqrt{x}\ge2-\sqrt{x}\) nên:
\(\Leftrightarrow2+\sqrt{x}+2-\sqrt{x}-2\sqrt{4-x}=2\)
\(\Leftrightarrow\sqrt{4-x}=1\)
\(\Rightarrow x=3\)

Đổi 1h30' = 1,5h
2h6' = 2,1h
Tốc độ xuôi dòng của cano là:
\(42:1,5=28\)\((km/h)\)
Tốc độ ngược dòng của cano là:
\(42:2,1=20(km/h)\)
Tốc độ khi nước yên lặng là
\(\left(28+20\right):2=24\) \((km/h)\)
Tốc độ dòng nước là:
\(28 - 24 = 4(km/h)\)
Đáp số:...

Gọi tỉ lệ cắt giảm mỗi năm của công ty là \(x\left(\%\right)\) hay \(\dfrac{x}{100}\) với \(0\le x\le100\)
Số công nhân còn lại sau năm thứ nhất là:
\(10000\left(1-\dfrac{x}{100}\right)\)
Số công nhân còn lại sau năm thứ hai là:
\(10000.\left(1-\dfrac{x}{100}\right)\left(1-\dfrac{x}{100}\right)=10000.\left(1-\dfrac{x}{100}\right)^2\)
Do sau 2 năm công ty còn lại 9000 công nhân nên:
\(10000\left(1-\dfrac{x}{100}\right)^2=9000\)
\(\Rightarrow1-\dfrac{x}{100}=\dfrac{3}{\sqrt{10}}\Rightarrow x=100-30\sqrt{10}\) (%)\(\approx5,13\left(\%\right)\)

a.
- Với \(y\ge0\Rightarrow x^2+2y\ge0\) với mọi x \(\Rightarrow\) hệ vô nghiệm do \(-2< 0\)
- Với \(y< 0\Rightarrow\left|y\right|=-y\), hệ tương đương:
\(\left\{{}\begin{matrix}x^2+2y=-2\\3x^2-y=15\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2+2y=-2\\6x^2-2y=30\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+2y=-2\\7x^2=28\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2=4\\y=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\pm2\\y=-3\end{matrix}\right.\)
b.
Gọi số chính phương cần tìm là \(n^2\) với n là số tự nhiên, do \(n^2\) có 4 chữ số
\(\Rightarrow999< n^2< 10000\Rightarrow31< n< 100\)
Do khi cộng số cần tìm với 2023 ta cũng được 1 SCP
\(\Rightarrow n^2+2023=m^2\) (với m tự nhiên và \(m>n\))
\(\Rightarrow m^2-n^2=2023\)
\(\Rightarrow\left(m-n\right)\left(m+n\right)=2023\)
Ta chỉ cần xét các cặp ước của 2023 mà \(m+n>m-n\)
| m-n | 1 | 7 | 17 |
| m+n | 2023 | 289 | 119 |
| m | 1012 | 148 | 68 |
| n | 1011 | 141 | 51 |
Do \(31< n< 100\) nên chỉ có \(n=51\) thỏa mãn
Vậy số cần tìm là \(51^2=2601\)