
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đề 1:
Bài 1:
\(a,=\sqrt{\left(\sqrt{7}+1\right)^2}-\left|-1+\sqrt{7}\right|=\sqrt{7}+1-\sqrt{7}+1=2\\ b,=2\sqrt{2}-4\sqrt{2}-5\sqrt{2}+\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}-7\sqrt{2}=\dfrac{-13\sqrt{2}}{\sqrt{2}}\)
Bài 2:
\(PT\Leftrightarrow\sqrt{\left(x-\dfrac{1}{2}\right)^2}=\dfrac{1}{2}\Leftrightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}+\dfrac{1}{2}=1\\x=-\dfrac{1}{2}+\dfrac{1}{2}=0\end{matrix}\right.\)
Bài 3:
\(a,M=\dfrac{a-2\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{2\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)^2\left(\sqrt{a}+1\right)}=\dfrac{2}{\sqrt{a}+1}\\ b,M< 1\Leftrightarrow\dfrac{2}{\sqrt{a}+1}-1< 0\Leftrightarrow\dfrac{1-\sqrt{a}}{\sqrt{a}+1}< 0\\ \Leftrightarrow1-\sqrt{a}< 0\left(\sqrt{a}+1>0\right)\\ \Leftrightarrow a>1\)




gọi độ cao của vệ tinh C so với mặt đất là đoạn CH
lại có AB+BH=AH<=>AH=110+BH(4)
xét tam giác ACH vuông tại H có: \(tan83,9^o=\dfrac{CH}{AH}=>CH=AH.tan83,9^o\left(1\right)\)
xét tam giác CBH vuông tại H có: \(tan86,2^o=\dfrac{CH}{BH}=>CH=BH.tan86,2^o\left(2\right)\)
(1)(2)=>\(BH.tan86,2^o=AH.tan83,9^o\)
mà AH=110+BH(cmt)=>\(BH.tan86,2^o=\left(110+BH\right)tan83,9^o\)
\(=>BH=180,6cm\)(3)
thay (3) vào(2)=>\(CH=\)\(180,6.tan86,2^o=2719,5km\)
vậy độ cao vệ tinh C là 2719,5km


ĐKXĐ: x>=0; x<>9
\(B=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{-3\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{1}{\sqrt{x}+1}=\dfrac{-3}{\sqrt{x}+3}\)

Mỗi một tháng người đó nhận được số tiền lãi là: \(100\cdot1,1\%=1,1\left(tr\right)\)
a) Đổi: 4 năm = 48 tháng
=> Sau 4 năm người đó thu về số tiền là:
$sau 4 năm = $gốc + $lãi
= 100 + 48 . 1,1 = 152,8 (triệu)
b) Mỗi tháng người đó mất: 4 - 1,1 = 2,9 (triệu)
=> Số tháng mà người đó sẽ tiêu hết số tiền là: 100 : 2,9 \(\cong34,5\left(th\right)\)






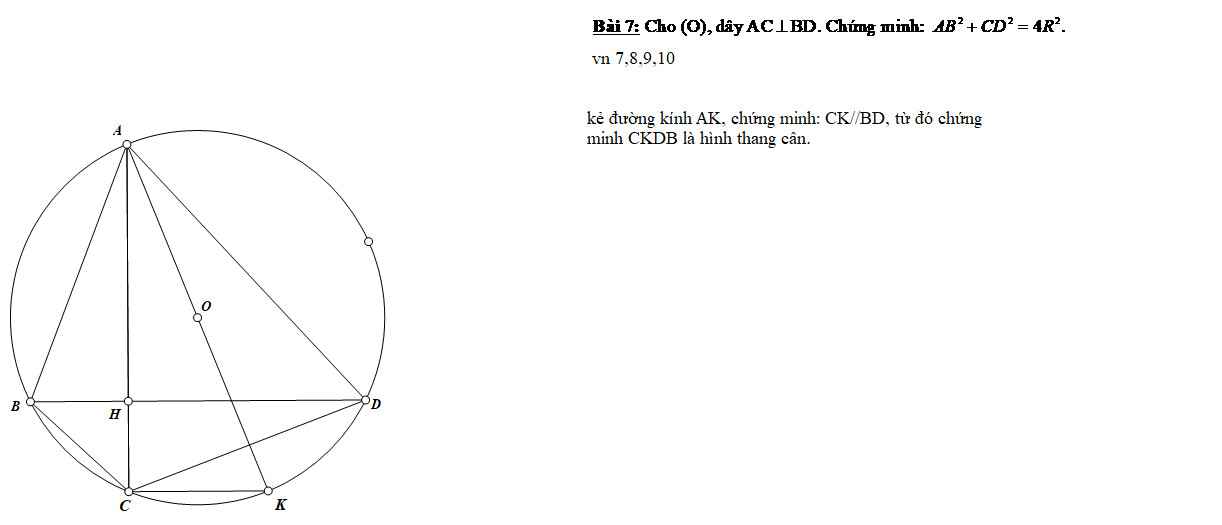



 Mọi người ơi,giúp em bài với ạ em cảm ơn ạ
Mọi người ơi,giúp em bài với ạ em cảm ơn ạ
Đổi 1h30' = 1,5h
2h6' = 2,1h
Tốc độ xuôi dòng của cano là:
\(42:1,5=28\)\((km/h)\)
Tốc độ ngược dòng của cano là:
\(42:2,1=20(km/h)\)
Tốc độ khi nước yên lặng là
\(\left(28+20\right):2=24\) \((km/h)\)
Tốc độ dòng nước là:
\(28 - 24 = 4(km/h)\)
Đáp số:...
UP