\(\Delta\)ABC vuông tại A, đường phân giác BE(E ϵ AC) . Kẻ EH \(\perp\) BC ( H ϵ BC). Gọi K là giao điểm của AB và HE . Chứng minh rằng AH\(//\) KC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
7 tháng 5
a: Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
\(\widehat{ABH}=\widehat{DBH}\)
Do đó: ΔBAH=ΔBDH
b: ΔBAH=ΔBDH
=>BA=BD và HA=HD
ta có:BA=BD
=>B nằm trên đường trung trực của AD(1)
ta có: HA=HD
=>H nằm trên đường trung trực của AD(2)
Từ (1),(2) suy ra BH là đường trung trực của AD
d: Gọi M là giao điểm của CK với BA
Xét ΔBMC có
BK,CA là các đường cao
BK cắt CA tại H
Do đó: H là trực tâm của ΔBMC
=>MH\(\perp\)BC
mà HD\(\perp\)BC
nên M,H,D thẳng hàng
=>BA,DH,CK đồng quy
7 tháng 5
a: R(x)-S(x)
\(=2x^3+x^2+x+2-x^3-x^2+x-2\)
\(=x^3+2x\)
R(x)+S(x)
\(=2x^3+x^2+x+2+x^3+x^2-x+2\)
\(=3x^3+2x^2+4\)
b: Đặt R(x)-S(x)=0
=>\(x^3+2x=0\)
=>\(x\left(x^2+2\right)=0\)
mà \(x^2+2>=2>0\forall x\)
nên x=0
7 tháng 5
a: Xét ΔNMA vuông tại M và ΔNBA vuông tại B có
NA chung
\(\widehat{MNA}=\widehat{BNA}\)
Do đó: ΔNMA=ΔNBA
b: ΔNMA=ΔNBA
=>NM=NB
c: Ta có: ΔNMA=ΔNBA
=>AM=AB
=>A nằm trên đường trung trực của MB(1)
Ta có: NM=NB
=>N nằm trên đường trung trực của MB(2)
Từ (1),(2) suy ra NA là đường trung trực của MB
d: Xét ΔNCK có
CB,KM là các đường cao
CB cắt KM tại A
Do đó: A là trực tâm của ΔNCK
=>NA\(\perp\)CK
NH
1
7 tháng 5
Câu 3:
1: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC
=>\(AD=AE\)
2: Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
mà HK\(\perp\)BC
nên A,H,K thẳng hàg
=>AK\(\perp\)BC tại K
ΔABC cân tại A
mà AK là đường cao
nên AK là phân giác của góc BAC
Câu 4:
\(f\left(-1\right)\cdot f\left(2\right)\)
\(=\left(-a+b-c+d\right)\cdot\left(8a+4b+2c+d\right)\)
\(=\left(-a+b+c-2c+d\right)\left(8a+4b+4c-2c+d\right)\)
\(=\left(-a-3a-2c+d\right)\left(8a+4\cdot\left(-3a\right)-2c+d\right)\)
\(=\left(-4a-2c+d\right)\left(-4a-2c+d\right)=\left(-4a-2c+d\right)^2\) là bình phương của một số nguyên
6 tháng 5
x=2022 nên x+1=2023
\(M\left(x\right)=x^{2023}-2023\left(x^{2022}-x^{2021}+x^{2020}-...+x^2-x\right)\)
\(=x^{2023}-\left(x+1\right)\left(x^{2022}-x^{2021}+...+x^2-x\right)\)
\(=x^{2023}-x^{2023}-x^{2022}+x^{2022}+x^{2021}+...-x^3-x^2+x^2+x\)
=x
=2022
7 tháng 5
a: Sửa đề: ΔAKB và ΔAKC
Xét ΔAKB và ΔAKC có
AK chung
\(\widehat{KAB}=\widehat{KAC}\)
AB=AC
Do đó: ΔAKB=ΔAKC
b: ΔAKB=ΔAKC
=>KB=KC
=>ΔKBC cân tại K
c: Ta có: ΔABC cân tại A
mà AD là đường phân giác
nên AD\(\perp\)BC
LH
1
6 tháng 5
\(x^2\left(x+y\right)-y^2\left(x+y\right)+2\left(x^2+y^2\right)+2\left(x+y\right)\)
\(=-2x^2+2y^2+2x^2+2y^2+2\left(x+y\right)\)
\(=4y^2+2\cdot\left(-2\right)=4y^2-4\)
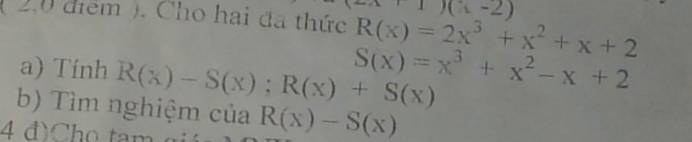
Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
=>BA=BH và EA=EH
Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)(hai góc đối đỉnh)
Do đó: ΔEAK=ΔEHC
=>AK=HC
Xét ΔBKC có \(\dfrac{BA}{AK}=\dfrac{BH}{HC}\)
nên AH//KC