a) Sửa: \(\dfrac{x-2}{x+2}+\dfrac{x}{2-x}+\dfrac{8}{x^2-4}\left(x\ne\pm2\right)\) 

\(=\dfrac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x}{x-2}+\dfrac{8}{\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{x^2-4x+4+8}{\left(x+2\right)\left(x-2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)

\(=\dfrac{x^2-4x+12-x^2-2x}{\left(x+2\right)\left(x-2\right)}\)

\(=\dfrac{-6x+12}{\left(x+2\right)\left(x-2\right)}\)

\(=\dfrac{-6\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}\)

\(=\dfrac{-6}{x+2}\)

b) \(\dfrac{x}{x-2}+\dfrac{2-x}{x+2}+\dfrac{12-10x}{x^2-4}\left(x\ne\pm2\right)\)

\(=\dfrac{x\left(x+2\right)}{\left(x+2\right)\left(x+2\right)}-\dfrac{x-2}{x+2}+\dfrac{12-10x}{\left(x+2\right)\left(x-2\right)}\)

\(=\dfrac{x^2+2x+12-10x}{\left(x+2\right)\left(x-2\right)}-\dfrac{\left(x-2\right)^2}{\left(x+2\right)\left(x+2\right)}\)

\(=\dfrac{x^2-8x+12-x^2+4x-4}{\left(x+2\right)\left(x-2\right)}\)

\(=\dfrac{-4x+8}{\left(x+2\right)\left(x-2\right)}\)

\(=\dfrac{-4\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}\)

\(=\dfrac{-4}{x-2}\)

c) \(C=\dfrac{2x}{x+3}+\dfrac{2}{x-3}+\dfrac{x^2-x+6}{9-x^2}\left(x\ne\pm3\right)\)

\(C=\dfrac{2x}{x+3}+\dfrac{2}{x-3}-\dfrac{x^2-x+6}{x^2-9}\)

\(C=\dfrac{2x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\dfrac{2\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{x^2-x+6}{\left(x+3\right)\left(x-3\right)}\)

\(C=\dfrac{2x^2-6x+2x+6-x^2+x-6}{\left(x+3\right)\left(x-3\right)}\)

\(C=\dfrac{x^2-3x}{\left(x+3\right)\left(x-3\right)}\)

\(C=\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}\)

\(C=\dfrac{x}{x+3}\)

\(\Leftrightarrow x\left(x+1\right)=y^2\)

+ Nếu \(y=0\)

\(\Rightarrow x\left(x+1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)

+ Nếu \(y\ne0\)

\(\Rightarrow\left\{{}\begin{matrix}x=y^m\\x+1=y^n\end{matrix}\right.\)

\(\Rightarrow x\left(x+1\right)=y^m.y^n=y^{m+n}=y^2\Rightarrow m+n=2\) (1)

Ta có

\(y^n-y^m=\left(x+1\right)-x=1\)

\(\Leftrightarrow y^n\left(1-y^{m-n}\right)=1.1\)

\(\Rightarrow\left\{{}\begin{matrix}y^n=1\\y^{m-n}=0\end{matrix}\right.\) (2)

Kết hợp (1) và (2)

\(\Rightarrow\left\{{}\begin{matrix}y^n=1\\y^{m-n}=0\\m+n=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n=0\\y=0\\m=2\end{matrix}\right.\) mâu thuẫn với đk \(y\ne0\)

\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\\y=0\end{matrix}\right.\)

Ta thấy: \(2024\equiv1\) (\(mod\) \(2023\))
\(20242024\equiv1909\) (\(mod\) \(2023\))
...
\(2024...2024:2023\) dư một số nào đó là một trong các số từ \(1\) đến \(2022\) (\(2023\) số).
* Xét \(2024\) số: \(2024;20242024;...;20242024...2024\) (Gồm \(2024\) bộ số \(2024\))
 + Lấy \(2024\) số trên chia cho \(2023\), ta có \(2024\) số dư từ \(0\) đến \(2022\).
\(\Rightarrow\) Tồn tại hai số chia cho \(2023\) có cùng số dư.
Giả sử hai số đó là \(a=2024...2024\) (\(i\) bộ số \(2024\)) và \(b=2024...2024\) (\(j\) bộ số \(2024\)) \(\left(1\le i\le j\le2024\right)\)
+ \(a-b=2024...2024\cdot10^{4i}\) (\(j-i\) bộ số \(2024\)) chia hết cho \(2023\)
+ \(ƯCLN\left(10^{4i};2023\right)=1\)
\(\Rightarrow2024...2024\) (\(j-i\) bộ số \(2024\)) chia hết cho \(2023\) \(\left(đpcm\right)\).

\(x^4-3x+2=x\left(x^3+ax^2+bx-2\right)-\left(x^3+ax^2+bx-2\right)\)

\(\Rightarrow x^4-3x+2=x^4+\left(a-1\right)x^3+\left(b-a\right)x^2-\left(b+2\right)x+2\)

Đồng nhất hệ số 2 vế ta được:

\(\left\{{}\begin{matrix}a-1=0\\b-a=0\\b+2=3\end{matrix}\right.\) \(\Rightarrow a=b=1\)

\(x^4-3x+2=\left(x-1\right)\left(x^3+ax^2+bx-2\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x^3+x^2+x-2\right)=\left(x-1\right)\left(x^3+ax^2+bx-2\right)\)
\(\Rightarrow x^3+x^2+x-2=x^3+ax^2+bx-2\)
\(\Rightarrow1\cdot x^2+1\cdot x=ax^2+bx\)
\(\Rightarrow a=1\) và \(b=1\)

Câu 1:

\(ĐK:x-2023\ne0\Leftrightarrow x\ne2023\) 

Câu 2: 

\(ĐK:x^2-9\ne0\Leftrightarrow x^2\ne9\Leftrightarrow x\ne\pm3\)

Câu 3: 

Phân thức đổi của phân thức `(-2y)/(5x^3)` là: `(2y)/(5x^3)` 

Câu 4:

\(\dfrac{1-x^2}{x\left(1-x\right)}=\dfrac{1^2-x^2}{x\left(1-x\right)}=\dfrac{\left(1-x\right)\left(1+x\right)}{x\left(1+x\right)}=\dfrac{1-x}{x}\left(x\ne0;x\ne1\right)\) 

Câu 5: 

ĐKXĐ: \(\left\{{}\begin{matrix}x-2\ne0\\x+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne-1\end{matrix}\right.\) 

Câu 6: 

\(\dfrac{x^2+y^2}{x-y}+\dfrac{-2xy}{x-y}=\dfrac{x^2-2xy+y^2}{x-y}=\dfrac{\left(x-y\right)^2}{x-y}=x-y\left(x\ne y\right)\) 

Câu 7: 

MTC là: \(5\left(x-3\right)\left(x+3\right)\)

Câu 8: 

\(\dfrac{2020^3-1}{2020^2+2021}=\dfrac{\left(2020-1\right)\left(2020^2+2020+1\right)}{2020^2+2020+1}=2020-1=2019\) 

Câu 9: 

\(\Delta ABC\sim\Delta PNM\)

Câu 10: 

Tỉ số đồng dạng:

\(\dfrac{A'B'}{AB}=\dfrac{1}{2}\) 

Câu 11:

Cần thêm đk: \(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}\) 

Câu 12: 

AD là tia phân giác của góc A ta có:

\(\dfrac{AB}{AC}=\dfrac{BD}{CD}\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{\sqrt{BC^2-AB^2}}=\dfrac{8}{\sqrt{10^2-8^2}}=\dfrac{8}{6}=\dfrac{4}{3}\)

\(A=\dfrac{x^2}{x^2-y^2-z^2}+\dfrac{y^2}{y^2-z^2-x^2}+\dfrac{z^2}{z^2-x^2-y^2}\)

\(=\dfrac{x^2}{\left(-y-z\right)^2-y^2-z^2}+\dfrac{y^2}{\left(-x-z\right)^2-z^2-x^2}+\dfrac{z^2}{\left(-x-y\right)^2-x^2-y^2}\)

\(=\dfrac{x^2}{2yz}+\dfrac{y^2}{2zx}+\dfrac{z^2}{2xy}=\dfrac{x^3+y^3+z^3}{3xyz}\)

\(=\dfrac{x^3+y^3+3xy\left(x+y\right)+z^3-3xy\left(x+y\right)}{2xyz}\)

\(=\dfrac{\left(x+y\right)^3+z^3-3xy.\left(-z\right)}{2xyz}\)

\(=\dfrac{\left(x+y+z\right)\left[\left(x+y\right)^2-z.\left(x+y\right)+z^2\right]+3xyz}{2xyz}\)

\(=\dfrac{0+3xyz}{2xyz}=\dfrac{3}{2}\)

Xét △ABC và △HBA có:
BAC=BHA(=90 độ)

ABC chung

=>ΔABC \(\sim\)ΔHBA

=>AB/HB=BC/BA

=>AB^2=HB.BC

Xét ΔHBA và ΔHAC có

AHB=AHC(=90 độ)

ABH=CAH(phụ BAH)

=>ΔHBA\(\sim\)ΔHAC

=>AH/CH=BH/AH

=>AH^2=BH.CH

c. Ta có: BM/MA=EB/EA

              AE/EC=BA/BC

             CN/BN=EC/BE

BM/MA.AE/EC.CN/BN=EB/EA.BA/BC.EC/BE

=>Để BM/MA.AE/EC.CN/BN=1 thì <=> EB/EA.BA/BC.EC/BE=1
(EB.BA.EC)/(EA.BC.BE)=1

<=>(BA.EC)/(EA.BC)=1

<=>BA.EC=EA.BC

<=>BA/BC=AE/EC
mà BA/BC=AE/EC(t/c đg phân giác)

=>BM/MA.AE/EC.CN/BN=1

\(B=3x^2+3y^2+z^2+5xy-3yz-3xz-2x-2y+3\\\Rightarrow4A=12x^2+12y^2+4z^2+20xy-12yz-12xz-8x-8y+12\\\\=[(9x^2+18xy+9y^2)-(12xz+12yz)+4z^2]+[(2x^2+4xy+2y^2)-(8x+8y)+8]+(x^2-2xy+y^2)+4\\=[(3x+3y)^2-2\cdot(3x+3y)\cdot2z+(2z)^2]+[2(x^2+2xy+y^2)-8(x+y)+8]+(x-y)^2+4\\=(3x+3y-2z)^2+2[(x+y)^2-4(x+y)+4]+(x-y)^2+4\\=(3x+3y-2z)^2+2(x+y-2)^2+(x-y)^2+4\)

Ta thấy: \(\left\{{}\begin{matrix}\left(3x+3y-2z\right)^2\ge0\forall x,y,z\\2\left(x+y-2\right)^2\ge0\forall x,y\\\left(x-y\right)^2\ge0\forall x,y\end{matrix}\right.\)

\(\Rightarrow\left(3x+3y-2z\right)^2+2\left(x+y-2\right)^2+\left(x-y\right)^2+4\ge4\forall x,y,z\)

\(\Leftrightarrow4B\ge4\Leftrightarrow B\ge1\)

Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}3x+3y-2z=0\\x+y-2=0\\x-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=x\\2x=2\\2z=6x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y=1\\z=3\end{matrix}\right.\)

Vậy \(Min_B=1\) khi \(x=y=1;z=3\).

\(Toru\)

a: Xét ΔBAC có AM là phân giác

nên \(\dfrac{BM}{MC}=\dfrac{AB}{AC}\)

=>\(\dfrac{BM}{MC}=\dfrac{a}{b}\)

=>\(\dfrac{BM}{a}=\dfrac{MC}{b}\)

mà BM+MC=BC=a

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{BM}{a}=\dfrac{MC}{b}=\dfrac{BM+MC}{a+b}=\dfrac{a}{a+b}\)

=>\(BM=\dfrac{a\cdot a}{a+b}=\dfrac{a^2}{a+b}\)

Xét ΔBCA có CN là phân giác

nên \(\dfrac{BN}{NA}=\dfrac{BC}{CA}\)

=>\(\dfrac{BN}{NA}=\dfrac{a}{b}\)

=>\(\dfrac{BN}{NA}=\dfrac{BM}{MC}\)

Xét ΔBAC có \(\dfrac{BN}{NA}=\dfrac{BM}{MC}\)

nên MN//AC

b: Xét ΔBAC có MN//AC

nên \(\dfrac{MN}{AC}=\dfrac{BM}{BC}\)

=>\(\dfrac{MN}{b}=\dfrac{a^2}{a+b}:a=\dfrac{a}{a+b}\)

=>\(MN=\dfrac{a\cdot b}{a+b}\)

a: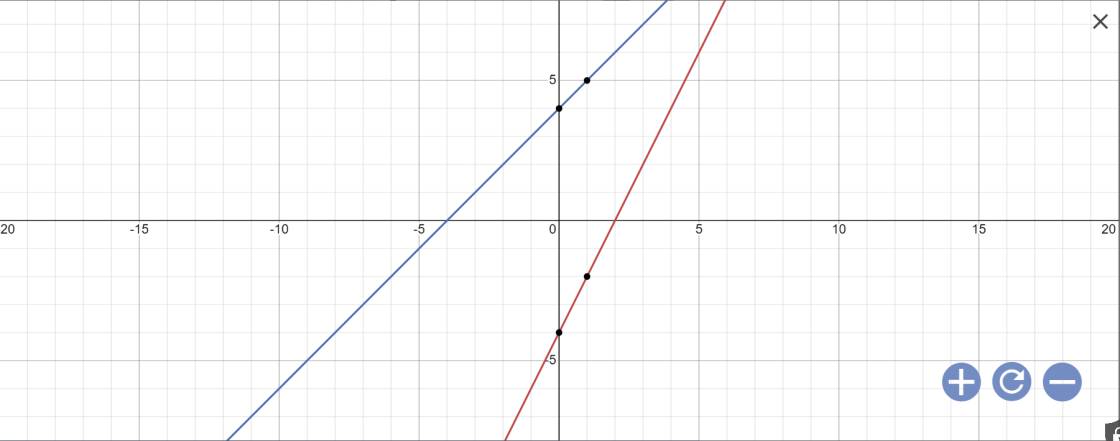 

b: Phương trình hoành độ giao điểm là:

2x-4=x+4

=>2x-x=4+4

=>x=8

Thay x=8 vào y=x+4, ta được:

y=8+4=12

Vậy: Q(8;12)

Tọa độ N là:

\(\left\{{}\begin{matrix}x=0\\y=2\cdot0-4=-4\end{matrix}\right.\)

Vậy: N(0;-4)

Tọa độ M là:

\(\left\{{}\begin{matrix}x=0\\y=0+4=4\end{matrix}\right.\)

Vậy: M(0;4)

M(0;4); N(0;-4); Q(8;12)

\(MN=\sqrt{\left(0-0\right)^2+\left(-4-4\right)^2}=8\)

\(MQ=\sqrt{\left(8-0\right)^2+\left(12-4\right)^2}=\sqrt{8^2+8^2}=8\sqrt{2}\)

\(NQ=\sqrt{\left(8-0\right)^2+\left(12+4\right)^2}=\sqrt{8^2+16^2}=8\sqrt{5}\)

Xét ΔMNQ có \(cosMNQ=\dfrac{NM^2+NQ^2-MQ^2}{2\cdot NM\cdot NQ}=\dfrac{256}{2\cdot8\cdot8\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)

=>\(sinMNQ=\sqrt{1-\left(\dfrac{2}{\sqrt{5}}\right)^2}=\dfrac{1}{\sqrt{5}}\)

Diện tích ΔMNQ là:

\(S_{MNQ}=\dfrac{1}{2}\cdot NM\cdot NQ\cdot sinMNQ\)

\(=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{5}}\cdot8\cdot8\sqrt{5}=\dfrac{64}{2}=32\)