Cho tam giác ABC và đường tròn nội tiếp (I). (I) tiếp xúc với BC, CA, AB lần lượt tại D, E, F. Gọi M và N lần lượt là trung điểm của BC và AI. Đường thẳng EI cắt DF tại P, đường thẳng FI cắt DE tại Q. Chứng minh rằng \(PQ\perp MN\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4b.
Gọi O là giao điểm AC và BD \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}\\\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}\end{matrix}\right.\)
\(T=\left(\overrightarrow{MO}+\overrightarrow{OA}\right)\left(\overrightarrow{MO}+\overrightarrow{OC}\right)+\left(\overrightarrow{MO}+\overrightarrow{OB}\right)^2+\left(\overrightarrow{MO}+\overrightarrow{OD}\right)^2\)
\(=3MO^2+\overrightarrow{MO}.\left(\overrightarrow{OA}+\overrightarrow{OC}\right)+\overrightarrow{OA}.\overrightarrow{OC}+OB^2+OD^2+2\overrightarrow{MO}\left(\overrightarrow{OB}+\overrightarrow{OD}\right)\)
\(=3MO^2-OA^2+OB^2+OD^2\)
\(=3MO^2+OA^2\) (do \(OA=OB=OD\) theo t/c hình chữ nhật)
OA cố định nên T min khi \(MO^2\) min
\(\Rightarrow M\) là hình chiếu vuông góc của O lên cạnh hình chữ nhật
Mà \(AB>AD\)
\(\Rightarrow M\) là hình chiếu vuông góc của O lên AB hoặc AD
\(\Rightarrow M\) là trung điểm AB hoặc AD

ĐKXĐ: \(x\ge-\dfrac{4}{3}\)
\(\left(x^2+6x+13\right)\left(\dfrac{9\left(5x+9\right)-4\left(3x+4\right)}{3\sqrt{5x+9}+2\sqrt{3x+4}}\right)=33x+65\)
\(\Leftrightarrow\dfrac{\left(x^2+6x+9\right)\left(33x+65\right)}{3\sqrt{5x+9}+2\sqrt{3x+4}}=33x+65\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{65}{33}< -\dfrac{4}{3}\left(ktm\right)\\x^2+6x+9=3\sqrt{5x+9}+2\sqrt{3x+4}\left(1\right)\end{matrix}\right.\)
Xét (1)
\(\Leftrightarrow x^2+x+3\left(x+3-\sqrt{5x+9}\right)+2\left(x+2-\sqrt{3x+4}\right)=0\)
\(\Leftrightarrow x^2+x+\dfrac{3\left(x^2+x\right)}{x+3+\sqrt{5x+9}}+\dfrac{2\left(x^2+x\right)}{x+2+\sqrt{3x+4}}=0\)
\(\Leftrightarrow\left(x^2+x\right)\left(1+\dfrac{3}{x+3+\sqrt{5x+9}}+\dfrac{2}{x+2+\sqrt{3x+4}}\right)=0\)
\(\Leftrightarrow x^2+x=0\) (ngoặc phía sau luôn dương khi \(x\ge-\dfrac{4}{3}\))
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)

Câu 1:
PT $\Leftrightarrow 3x^2+6x+3=2x^2-5x+3$
$\Leftrightarrow x^2+11x=0$
$\Leftrightarrow x(x+11)=0$
$\Leftrightarrow x=0$ hoặc $x+11=0$
$\Leftrightarrow x=0$ hoặc $x=-11$
Thử lại thấy đều thỏa mãn.
Câu 2:
PT $\Leftrightarrow 2x^2-3x+1=x^2+2x-3$ (bình phương 2 vế)
$\Leftrightarrow x^2-5x+4=0$
$\Leftrightarrow (x-1)(x-4)=0$
$\Leftrightarrow x-1=0$ hoặc $x-4=0$
$\Leftrightarrow x=1$ hoặc $x=4$
Thử lại thấy đều thỏa mãn.
Vậy..........

Bạn xem lại đề bài nhé, vì thông thường phương trình hàm có 2 biến \(x,y\) chỉ có 1 phương trình thôi.
Hơn nữa nếu đề bài như thế này thì giải rất dễ. Từ pt thứ hai cho \(x=c\) với c là hằng số bất kì thì thu được \(f\left(y\right)=2y+C,\forall x,y\inℝ^+\left(C=-f\left(c\right)\right)\) là hàm số bậc nhất. Thay lại vào pt đầu tiên thì thấy vô lí.
Nên mình nghĩ đề bài có thể là
"\(f\left(x+3f\left(y\right)\right)=f\left(x\right)+f\left(y\right)\pm2y,\forall x,y\inℝ^+\)

Theo định lý Vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{3b}{2a}\\x_1x_2=\dfrac{2c}{a}\end{matrix}\right.\)
Do đó \(T=\left|x_1-x_2\right|\)
\(=\sqrt{\left(x_1-x_2\right)^2}\)
\(=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\left(-\dfrac{3b}{2a}\right)^2-4.\dfrac{2c}{a}}\)
\(=\sqrt{\left(\dfrac{3b}{2a}\right)^2-\dfrac{8c}{a}}\)
Ta có \(a+9b+24c=0\)
\(\Leftrightarrow1+\dfrac{9b}{a}+\dfrac{24c}{a}=0\)
\(\Leftrightarrow\dfrac{24c}{a}=-\dfrac{9b}{a}-1\)
\(\Leftrightarrow\dfrac{8c}{a}=-\dfrac{3b}{a}-\dfrac{1}{3}\)
Do đó \(T=\sqrt{\left(\dfrac{3b}{2a}\right)^2+\dfrac{3b}{a}+\dfrac{1}{3}}\) \(\ge0\)
\(T=\sqrt{\left(\dfrac{3b}{2a}\right)^2+2.\dfrac{3b}{2a}+1-\dfrac{2}{3}}\)
\(T=\sqrt{\left(\dfrac{3b}{2a}+1\right)^2-\dfrac{2}{3}}\) \(\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow\left(\dfrac{3b}{2a}+1\right)^2=\dfrac{2}{3}\)
\(\Leftrightarrow...\)
Vậy ...

Đặt \(BC=x\left(cm\right)\) (ĐK: \(x>9\))
\(\Rightarrow AC=BC-9=x-9\left(cm\right)\)
Theo định lý Py-ta-go ta có:
\(BC^2=AC^2+AB^2\Rightarrow AB^2=BC^2-AC^2\)
\(\Rightarrow AB=\sqrt{x^2-\left(x-9\right)^2}=\sqrt{x^2-\left(x^2-18x+81\right)}\)
\(\Rightarrow AB=\sqrt{18x-81}\)
Theo đề bài: \(C_{ABC}=70\left(cm\right)\)
\(\Rightarrow AB+AC+BC=70\)
\(\Rightarrow\sqrt{18x-81}+\left(x-9\right)+x=70\)
\(\Rightarrow\sqrt{18x-81}=79-2x\left(x\le\dfrac{79}{2}\right)\)
\(\Rightarrow18x-81=\left(79-2x\right)^2\)
\(\Rightarrow18x-81=6241-316x+4x^2\)
\(\Rightarrow4x^2-334x+6322=0\)
\(\Delta=\left(-334\right)^2-4\cdot4\cdot6322=10404>0\)
\(x_1=\dfrac{334+\sqrt{10404}}{2\cdot4}=\dfrac{109}{2}>\dfrac{79}{2}\left(ktm\right)\)
\(x_2=\dfrac{334-\sqrt{10404}}{2\cdot4}=29\left(tm\right)\)
\(\Rightarrow BC=29\left(cm\right)\)
\(AC=29-9=20\left(cm\right)\)
\(AB=\sqrt{18\cdot29-81}=21\left(cm\right)\)
Vậy: ...

Vì sao trong trường hợp cả 2024 câu đã là đúng thì chính chúng lại là những câu sai ạ? Nếu vậy thì nó vô lý rồi ạ, vì một mệnh đề không thể vừa đúng vừa sai được.
Ta loại câu số 2024 vì nếu đây là khẳng định đúng thì số khẳng định sai nhiều nhất chỉ là 2023, không thể có tới 2024 khẳng định sai.
Xét câu 1: nếu có ít nhất 1 câu khẳng định sai thì khẳng định sai là câu 2024. Vậy thì câu 2 sẽ đúng, tuy nhiên câu thứ 2 mâu thuẫn với câu 1, vậy câu 1 sai.
Xét câu \(n\left(1< n< 2023\right)\), nếu có ít nhất n câu khẳng định sai thì khẳng định sai là câu \(1,...,n-1,2024\), Vậy thì câu \(n+1\) sẽ đúng, tuy nhiên câu thứ \(n+1\) mâu thuẫn với câu n, vậy câu n sai.
Sau khi loại từ câu 1 tới 2022 và câu 2024. Ta thấy có 2023 khẳng định sai, vậy câu 2023 đúng.

Giả sử có hữu hạn số nguyên tố là \(p_1,p_2,...,p_n\) với \(n\ge1\)
Gọi \(p_i\left(1\le i\le n\right)\) là số nguyên tố lớn nhất trong n số nguyên tố trên. Xét số \(P=p_1p_2...p_n+1\), rõ ràng \(P>p_i\) . Hơn nữa \(P\) không chia chết cho bất kì số nguyên tố \(p_j\left(1\le j\le n\right)\) nào nên \(P\) cũng là một số nguyên tố.
Như vậy, ta tìm được một số nguyên tố mới lớn hơn \(p_i\) là số nguyên tố lớn nhất. Điều này là vô lí.
Vậy điều giả sử là sai \(\Rightarrow\) Có vô hạn số nguyên tố.
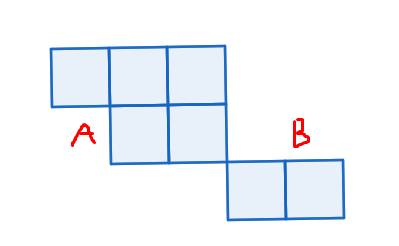
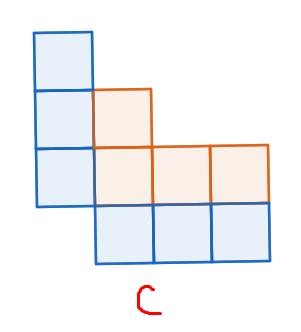

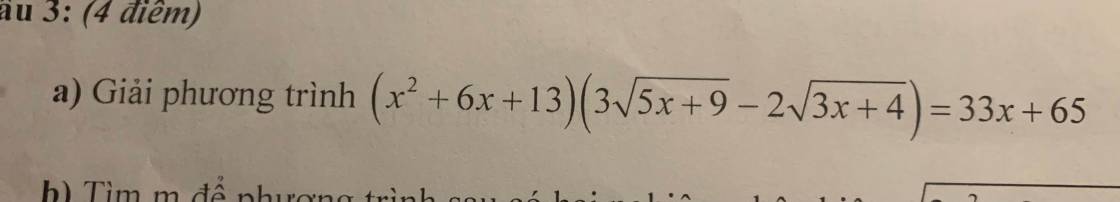
 Mọi người giúp em với ạ, giải chi tiết giúp em với :( em thật sự không hiểu mà tuần sau em thi r. Giúp em với m.ng aa
Mọi người giúp em với ạ, giải chi tiết giúp em với :( em thật sự không hiểu mà tuần sau em thi r. Giúp em với m.ng aa