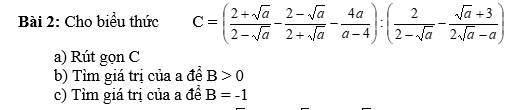ĐKXĐ: \(a\ne4\)

a) \(C=\left(\dfrac{2+\sqrt{a}}{2-\sqrt{a}}-\dfrac{2-\sqrt{a}}{2+\sqrt{a}}-\dfrac{4a}{a-4}\right):\left(\dfrac{2}{2-\sqrt{a}}-\dfrac{\sqrt{a}+3}{2\sqrt{a}-a}\right)\)

\(=\left[\dfrac{\left(2+\sqrt{a}\right)^2-\left(2-\sqrt{a}\right)^2}{\left(2+\sqrt{a}\right)\left(2-\sqrt{a}\right)}+\dfrac{4a}{4-a}\right]:\left[\dfrac{2\sqrt{a}-\sqrt{a}-3}{\sqrt{a}\left(2-\sqrt{a}\right)}\right]\)

\(=\dfrac{4+4\sqrt{a}+a-4+4\sqrt{a}-a+4a}{\left(2+\sqrt{a}\right)\left(2-\sqrt{a}\right)}.\dfrac{\sqrt{a}\left(2-\sqrt{a}\right)}{\sqrt{a}-3}\)

\(=\dfrac{4a+8\sqrt{a}}{\left(2+\sqrt{a}\right)\left(2-\sqrt{a}\right)}.\dfrac{\sqrt{a}\left(2-\sqrt{a}\right)}{\sqrt{a}-3}\)

\(=\dfrac{4\sqrt{a}\left(\sqrt{a}+2\right).\sqrt{a}\left(2-\sqrt{a}\right)}{\left(2+\sqrt{a}\right)\left(2-\sqrt{a}\right)\left(\sqrt{a}-3\right)}\)

\(=\dfrac{4a}{\sqrt{a}-3}\)

Biểu thức B là biểu thức nào vậy em?

1) \(y=mx+1\left(m\ne0\right)\left(1\right)\) hay \(mx-y+1=0\)

Để đồ thị hàm số \(\left(1\right)\) đi qua điểm \(M\left(-1;-1\right)\) khi và chỉ khi

\(m.\left(-1\right)+1=-1\)

\(\Leftrightarrow-m=-2\)

\(\Leftrightarrow m=2\)

Vậy hàm số \(\left(1\right):y=2x+1\)

Bạn tự vẽ đồ thị nhé!

2) \(y=\left(m^2-2\right)x+2m+3\left(d\right)\)

Để \(\left(1\right)//\left(d\right)\) khi và chỉ khi

\(\left\{{}\begin{matrix}m^2-2=2\\2m+3\ne1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\2m\ne-2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\ne-1\end{matrix}\right.\) \(\Leftrightarrow m=\pm2\) thỏa đề bài

3) Khoảng cách từ gốc O đến đồ thị hàm số \(\left(1\right)\) là:

\(d\left(O;\left(1\right)\right)=\dfrac{m.0-0+1}{\sqrt[]{2^2+1^2}}=\dfrac{2}{\sqrt[]{5}}\)

\(\Leftrightarrow\dfrac{0.m+1}{\sqrt[]{5}}=\dfrac{2}{\sqrt[]{5}}\)

\(\Leftrightarrow0m=1\)

\(\Leftrightarrow m\in\varnothing\)

Vậy không có giá trị nào của m để thỏa mãn đề bài,

Đáp án:

1. Tìm m để đồ thị hàm số (1) đi qua điểm M (−1;−1). Với m tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy

Để đồ thị hàm số (1) đi qua điểm M (−1;−1), ta cần có m(−1)+1=−1. Từ đó ta có m=−2.

Với m=−2, đồ thị hàm số (1) là một đường thẳng có hệ số góc -2 và đi qua điểm M (−1;−1). Ta có thể vẽ đồ thị hàm số như sau:

[Image of the graph of y=-2x+1]

2. Tìm giá trị của m để đồ thị hàm số (1) song song với đường thẳng y (m² - 2) x + 2m+3 =

Hai đường thẳng song song khi hệ số góc của chúng bằng nhau. Do đó, ta có m=m2−2. Từ đó ta có m=2.

3. Tìm m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng 2 √5

Khoảng cách từ gốc O đến đồ thị hàm số (1) là khoảng cách từ điểm (0;1) đến đường thẳng y=mx+1. Khoảng cách này được tính theo công thức:

Do đó, ta có d=2552=2.

Từ đó, ta có m=2.

Kết luận:

• Giá trị của m để đồ thị hàm số (1) đi qua điểm M (−1;−1) là m=-2.
• Giá trị của m để đồ thị hàm số (1) song song với đường thẳng y (m² - 2) x + 2m+3 = là m=2.
• Giá trị của m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng 2 √5 là m=2.

Lưu ý:

• Để giải bài toán 1 và 2, ta có thể thay m=-2 vào hàm số (1) và so sánh với tọa độ của điểm M (−1;−1) hoặc tọa độ của một điểm bất kỳ trên đường thẳng y (m² - 2) x + 2m+3 =.
• Để giải bài toán 3, ta có thể sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.

chúc bạn học tốt

Trên tia đối của tia \(AM\) lấy \(I\) sao cho: \(AI=CE\)

Xét \(\Delta ADI\) và \(\Delta CDE\) có:

\(AD=CD\left(gt\right)\)

\(\widehat{DAI}=\widehat{DCE}=90^o\)

\(AI=CE\left(gt\right)\)

Vậy \(\Delta ADI=\Delta CDE\left(c.g.c\right)\)

\(\Leftrightarrow\widehat{IDA}=\widehat{EDC}\) ( 2 góc t/ứng )

\(\Leftrightarrow\widehat{AID}=\widehat{CED}\) ( 2 góc t/ứng )

\(\Leftrightarrow\) \(\widehat{CED}=\widehat{ADE}\) mà 2 góc này ở vị trí so le trong ( do \(AD//BC\) )

\(\Rightarrow\widehat{AID}=\widehat{ADE}\left(1\right)\)

Ta có: \(\widehat{ADE}=\widehat{ADM}+\widehat{MDE}\left(2\right)\)

Vì \(\widehat{MDE}=\widehat{EDC}\)

\(\Rightarrow\widehat{MED}=\widehat{IDA}\left(3\right)\)

Từ \(\left(2\right);\left(3\right)\Rightarrow\widehat{ADE}=\widehat{ADM}+\widehat{IDA}=\widehat{IDM}\left(4\right)\)

Từ \(\left(1\right);\left(4\right)\Rightarrow\widehat{AID}=\widehat{IDM}\)

\(\Leftrightarrow\widehat{MID}=\widehat{IDM}\)

\(\Leftrightarrow\Delta IDM\) cân \(\left\{M\right\}\)

\(\Leftrightarrow DM=IM\)

Ta lại có: \(IM=AM+AI=AM+CE\)

\(\Rightarrow DM=AM+CE\)

Ta đặt:  \(S_{BEMF}=S_1;S_{ABC}=S\)

Kẻ \(AK\perp BC\) ; \(AK\) cắt \(EM\left\{H\right\}\)

Ta có: \(S_1=EM.HK\)

\(\Leftrightarrow S=\dfrac{1}{2}BC.AK\)

\(\Leftrightarrow\dfrac{S_1}{S}=2\dfrac{EM}{BC}.\dfrac{KH}{AK}\)

Đặt \(MA=x;MC=y\) . Theo định lý Thales ta có:

\(\dfrac{EM}{BC}=\dfrac{x}{x+y};\dfrac{HK}{AK}=\dfrac{x}{x+y}\)

\(\Leftrightarrow\dfrac{S_1}{S}=\dfrac{2xy}{\left(x+y\right)^2}\)

Áp dụng bất đẳng thức Cosi dạng \(\dfrac{ab}{\left(a+b\right)^2}\le\dfrac{1}{4}\) ta được:

\(\dfrac{S_1}{S}=\dfrac{2xy}{\left(x+y\right)^2}\le\dfrac{1}{2}\) hay \(S_1\le\dfrac{1}{2}S\)

\(\Leftrightarrow MaxS_1=\dfrac{1}{2}S\)

\(\Leftrightarrow\) \(M\) là trung điểm của \(AC\)

Bạn xem lại đề bài.

Bạn xem lại đề

\(A=\sqrt[]{1+2015^2+\dfrac{2015^2}{2016^2}}+\dfrac{2015}{2016}\)

\(\Leftrightarrow A=\sqrt[]{\left(1+2015\right)^2-2.2015+\dfrac{2015^2}{\left(2015+1\right)^2}}+\dfrac{2015}{2016}\)

\(\Leftrightarrow A=\sqrt[]{\left(1+2015-\dfrac{2015}{2015+1}\right)^2}+\dfrac{2015}{2016}\)

\(\Leftrightarrow A=\left|1+2015-\dfrac{2015}{2016}\right|+\dfrac{2015}{2016}\)

\(\Leftrightarrow A=1+2015-\dfrac{2015}{2016}+\dfrac{2015}{2016}\)

\(\Leftrightarrow A=1+2015=2016\)

Lời giải:

Đặt $x=a; \frac{y}{2}=b$ thì bài toán trở thành:

Tìm min $A=\frac{1}{a^2+1}+\frac{1}{b^2+1}+2ab$ với $ab\geq 1$
----------------------------------

Với $ab\geq 1$, ta có BĐT khá quen thuộc:

$\frac{1}{a^2+1}+\frac{1}{b^2+1}\geq \frac{2}{ab+1}$ (để cm BĐT này bạn chỉ cần biến đổi tương đương) 

Áp dụng vào bài và sử dụng thêm BĐT AM-GM:

$A\geq \frac{2}{ab+1}+2ab=\frac{2}{ab+1}+\frac{ab+1}{2}+\frac{3ab-1}{2}$

$\geq 2\sqrt{\frac{2}{ab+1}.\frac{ab+1}{2}}+\frac{3ab-1}{2}$

$=2+\frac{3ab-1}{2}\geq 2+\frac{3.1-1}{2}=3$

Vậy $A_{\min}=3$.

Đặt \(A=\sqrt{a+1}+\sqrt{a+3}\)

\(\Rightarrow A^2=2a+4+2\sqrt{\left(a+1\right)\left(a+3\right)}\)

Đặt \(B=2\sqrt{a+2}\)

\(\Rightarrow B^2=4a+8\)

Xét hiệu \(B^2-A^2=2a+4-2\sqrt{\left(a+1\right)\left(a+3\right)}\)

Áp dụng BĐT Cô-si, ta có \(2a+4=\left(a+1\right)+\left(a+3\right)\) \(>2\sqrt{\left(a+1\right)\left(a+3\right)}\) 

 (Dấu "=" không thể xảy ra vì khi đó sẽ suy ra đẳng thức vô lí là \(1=3\))

 Từ đó suy ra \(B^2-A^2>0\) \(\Leftrightarrow B^2>A^2\), và do A, B dương nên suy ra \(B>A\). Nói cách khác, \(2\sqrt{a+2}>\sqrt{a+1}+\sqrt{a+3}\)

sao em bấm máy tính thì dấu bằng $x$ảy ra khi $x$=10000000 vậy ạ.