Đặt \(x^2+y^2=a\)

Khi đó ta được: \(P=\left(a+2\right)^3-\left(a-2\right)^3-12a^2\)

\(\Leftrightarrow P=a^3.6a^2+12a+8-a^3+6a^2-12a+8-12a^2\)

\(\Leftrightarrow P=\left(a^3-a^3\right)+\left(6a^2+6a^2-12a^2\right)+\left(12a-12a\right)+8+8\)

\(\Leftrightarrow P=16\)

Vậy \(P=16\) tại \(x=2019\) và \(y=2020\)

a)Ta có:

AO=BO=OC=DO (vì O là trung điểm của AC và BD)

AH=HI=IL=KL (vì H, I, K, L lần lượt là hình chiếu của O trên AB, BC, CD, DA)

AO=AH+HO

BO=HI+HO

CO=IL+HO

DO=KL+HO

AH+HO=HI+HO=IL+HO=KL+HO

AH=HI=IL=KL

Vậy, bốn đoạn thẳng AH, HI, IL, KL bằng nhau và có chung điểm cuối H. Do đó, bốn điểm H, I, K, L cùng nằm trên một đường tròn có tâm O.

b) Ta có:

AH=HI=IL=KL=AC/2

AO=BO=OC=DO=AC/2

Gọi r là bán kính của đường tròn (O).

Từ các kết quả trên, ta có:

r=AC/2=4cm/2=2cm

Vậy, bán kính của đường tròn (O) là 2cm.

Bạn xem lại đề không hiểu các dâu hình chữ nhật sau ACB là gì?

Xét (O) có

EB,EI là tiếp tuyến

=>EB=EI

Xét (O) có

FI,FC là tiếp tuyến

=>FI=FC

BE+CF=EI+FI=EF

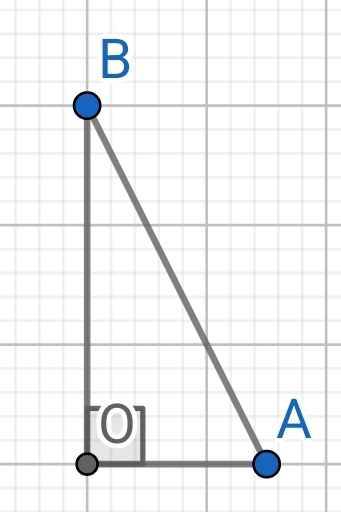  Thang chạm tường ở điểm B như trên hình.

⇒ OB là độ cao cần tính

Ta có:

sin A = OB/AB

⇒ OB = AB . sin A

= 5 . sin 65⁰

≈ 4,5 (m)

Theo đề bài : \(l=5\left(m\right);\alpha=65^o\) (\(\alpha\) là góc tạo bởi chân thang và mặt đất)

Thang chạm tường ở độ cao \(h\) so với mặt đất là :

\(sin\alpha=\dfrac{h}{l}\Rightarrow h=l.sin\alpha=5.sin65^o\sim4,5\left(m\right)\)

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có

góc DAB chung

Do đó: ΔADB đồng dạng với ΔAEC

b: 

ΔADB đồng dạng với ΔAEC

=>AD/AE=AB/AC

=>AE*AC=AE*AB

ΔANB vuông tại N có NE là đường cao

nên AE*AB=AN^2

ΔAMC vuông tại M có MD là đường cao

nên AD*AC=AM^2

mà AE*AB=AD*AC

nên AM=AN

1) \(\sqrt[]{9\left(x-1\right)}=21\)

\(\Leftrightarrow9\left(x-1\right)=21^2\)

\(\Leftrightarrow9\left(x-1\right)=441\)

\(\Leftrightarrow x-1=49\Leftrightarrow x=50\)

2) \(\sqrt[]{1-x}+\sqrt[]{4-4x}-\dfrac{1}{3}\sqrt[]{16-16x}+5=0\)

\(\Leftrightarrow\sqrt[]{1-x}+\sqrt[]{4\left(1-x\right)}-\dfrac{1}{3}\sqrt[]{16\left(1-x\right)}+5=0\)

\(\)\(\Leftrightarrow\sqrt[]{1-x}+2\sqrt[]{1-x}-\dfrac{4}{3}\sqrt[]{1-x}+5=0\)

\(\Leftrightarrow\sqrt[]{1-x}\left(1+3-\dfrac{4}{3}\right)+5=0\)

\(\Leftrightarrow\sqrt[]{1-x}.\dfrac{8}{3}=-5\)

\(\Leftrightarrow\sqrt[]{1-x}=-\dfrac{15}{8}\)

mà \(\sqrt[]{1-x}\ge0\)

\(\Leftrightarrow pt.vô.nghiệm\)

3) \(\sqrt[]{2x}-\sqrt[]{50}=0\)

\(\Leftrightarrow\sqrt[]{2x}=\sqrt[]{50}\)

\(\Leftrightarrow2x=50\Leftrightarrow x=25\)

1) \(\sqrt{9\left(x-1\right)}=21\) (ĐK: \(x\ge1\))

\(\Leftrightarrow3\sqrt{x-1}=21\)

\(\Leftrightarrow\sqrt{x-1}=7\)

\(\Leftrightarrow x-1=49\)

\(\Leftrightarrow x=49+1\)

\(\Leftrightarrow x=50\left(tm\right)\)

2) \(\sqrt{1-x}+\sqrt{4-4x}-\dfrac{1}{3}\sqrt{16-16x}+5=0\) (ĐK: \(x\le1\))

\(\Leftrightarrow\sqrt{1-x}+2\sqrt{1-x}-\dfrac{4}{3}\sqrt{1-x}+5=0\)

\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}+5=0\)

\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}=-5\) (vô lý) 

Phương trình vô nghiệm

3) \(\sqrt{2x}-\sqrt{50}=0\) (ĐK: \(x\ge0\)) 

\(\Leftrightarrow\sqrt{2x}=\sqrt{50}\)

\(\Leftrightarrow2x=50\)

\(\Leftrightarrow x=\dfrac{50}{2}\)

\(\Leftrightarrow x=25\left(tm\right)\)

4) \(\sqrt{4x^2+4x+1}=6\)

\(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\)

\(\Leftrightarrow\left|2x+1\right|=6\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\left(ĐK:x\ge-\dfrac{1}{2}\right)\\2x+1=-6\left(ĐK:x< -\dfrac{1}{2}\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=5\\2x=-7\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(tm\right)\\x=-\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)

5) \(\sqrt{\left(x-3\right)^2}=3-x\)

\(\Leftrightarrow\left|x-3\right|=3-x\)

\(\Leftrightarrow x-3=3-x\)

\(\Leftrightarrow x+x=3+3\)

\(\Leftrightarrow x=\dfrac{6}{2}\)

\(\Leftrightarrow x=3\)

a) \(\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}\)

\(=\sqrt{\left(\sqrt{2}\right)^2+2\sqrt{2}\cdot1+1^2}+\left|\sqrt{2}-2\right|\)

\(=\sqrt{\left(\sqrt{2}+1\right)^2}-\left(\sqrt{2}-2\right)\)

\(=\left|\sqrt{2}+1\right|-\sqrt{2}+2\)

\(=\sqrt{2}+1-\sqrt{2}+2\)

\(=3\)

b) \(\dfrac{1}{5}\sqrt{50}-2\sqrt{96}-\dfrac{\sqrt{30}}{\sqrt{15}}+12\sqrt{\dfrac{1}{6}}\)

\(=\dfrac{1}{5}\cdot5\sqrt{2}-2\cdot4\sqrt{6}-\sqrt{\dfrac{30}{15}}+\sqrt{\dfrac{144}{6}}\)

\(=\sqrt{2}-8\sqrt{6}-\sqrt{2}+2\sqrt{6}\)

\(=-8\sqrt{6}+2\sqrt{6}\)

\(=-6\sqrt{6}\)

c) \(\left(\dfrac{5-\sqrt{5}}{\sqrt{5}}-2\right)\left(\dfrac{4}{1+\sqrt{5}}+4\right)\)

\(=\left[\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{\sqrt{5}}-2\right]\left[\dfrac{4\left(1-\sqrt{5}\right)}{\left(1+\sqrt{5}\right)\left(1-\sqrt{5}\right)}+4\right]\)

\(=\left(\sqrt{5}-1-2\right)\left(\dfrac{4\left(1-\sqrt{5}\right)}{1-5}+4\right)\)

\(=\left(\sqrt{5}-3\right)\left(\sqrt{5}-1+4\right)\)

\(=\left(\sqrt{5}-3\right)\left(\sqrt{5}+3\right)\)

\(=\left(\sqrt{5}\right)^2-3^2\)

\(=-4\)

a) \(\sqrt[]{3+2\sqrt[]{2}}+\sqrt[]{\left(\sqrt[]{2}-2\right)^2}\)

\(=\sqrt[]{2+2\sqrt[]{2}.1+1}+\left|\sqrt[]{2}-2\right|\)

\(=\sqrt[]{\left(\sqrt[]{2}+1\right)^2}+\left(2-\sqrt[]{2}\right)\) \(\left(\left(\sqrt[]{2}\right)^2=2< 2^2=4\right)\)

\(=\left|\sqrt[]{2}+1\right|+2-\sqrt[]{2}\)

\(=\sqrt[]{2}+1+2-\sqrt[]{2}\)

\(=3\)

a) \(A=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{a-\sqrt{a}}\right):\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\right)\)

\(A=\left[\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right]:\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\right)\)

\(A=\left[\dfrac{a}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right]:\left[\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\right]\)

\(A=\dfrac{a-1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\left[\dfrac{\sqrt{a}-1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}+\dfrac{2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right]\)

\(A=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{\sqrt{a}-1+2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)

\(A=\dfrac{\sqrt{a}+1}{\sqrt{a}}:\dfrac{\sqrt{a}+1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)

\(A=\dfrac{\sqrt{a}+1}{\sqrt{a}}\cdot\left(\sqrt{a}-1\right)\)

\(A=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\sqrt{a}}\)

\(A=\dfrac{a-1}{\sqrt{a}}\)

b) Ta có:

\(a=4+2\sqrt{3}=\left(\sqrt{3}\right)^2+2\sqrt{3}\cdot1+1^2=\left(\sqrt{3}+1\right)^2\)

Thay vào A ta có:

\(A=\dfrac{\left(\sqrt{3}+1\right)^2-1}{\sqrt{\left(\sqrt{3}+1\right)^2}}=\dfrac{4+2\sqrt{3}-1}{\sqrt{3}+1}=\dfrac{3+2\sqrt{3}}{\sqrt{3}+1}\) 

c) \(A< 0\) khi:

\(\dfrac{a-1}{\sqrt{a}}< 0\)

Mà: \(\sqrt{a}\ge0\forall x\) (xác định) 

\(\Leftrightarrow a-1< 0\)

\(\Leftrightarrow a< 1\)

Kết hợp với đk:

\(0< a< 1\)

\(\left(x^2-\dfrac{y}{2}\right)^3\)

\(=\left(x^2\right)^3-3\cdot\left(x^2\right)^2\cdot\dfrac{y}{2}+3\cdot x^2\cdot\left(\dfrac{y}{2}\right)^2-\left(\dfrac{y}{2}\right)^3\)

\(=x^6-\dfrac{3x^4y}{2}+\dfrac{3x^2y^2}{4}-\dfrac{y^3}{8}\)