Chứng minh rằng:(2n+3)2-(2n-1)2 chia hết cho 8 với n \(\in\) Z
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



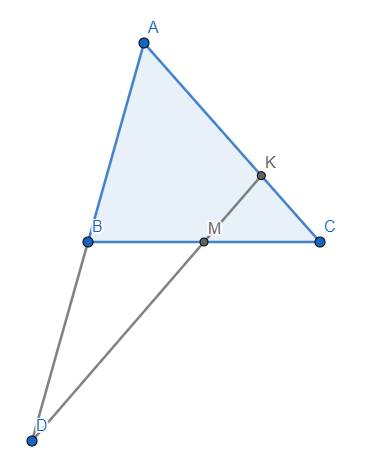
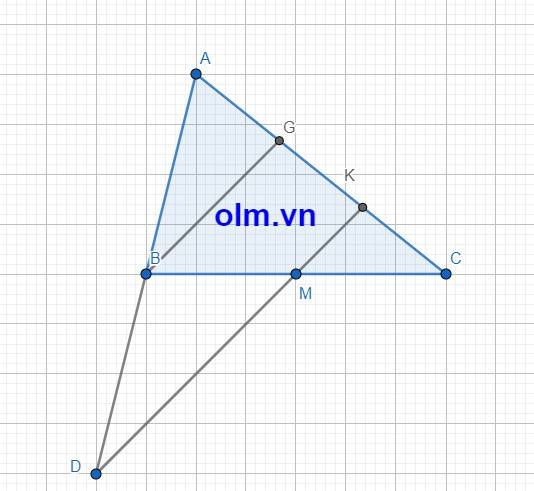
Bài này có thể giải bằng cách dùng định lý Menelaus khá ngắn như sau:
Áp dụng định lý Menelaus cho tam giác ABC với cát tuyến DMK, ta có: \(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{AB}=1\) \(\Rightarrow1.\dfrac{KC}{KA}.2=1\) \(\Leftrightarrow\dfrac{KC}{KA}=\dfrac{1}{2}\) \(\Leftrightarrow KA=2KC\) (đpcm)
Nhưng nếu bạn chưa được dùng định lý Menelaus thì sẽ phải làm như sau:
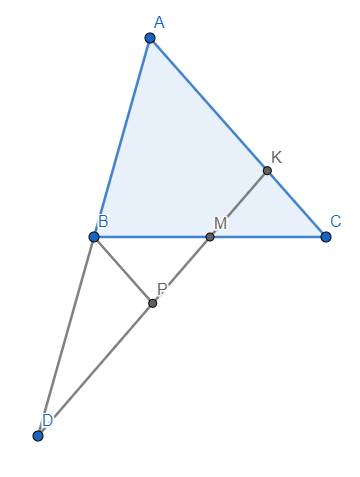
Kẻ BP//AC \(\left(P\in DK\right)\). Khi đó theo định lý Thales, \(\dfrac{MB}{MC}=\dfrac{BP}{CK}\) và \(\dfrac{DA}{DB}=\dfrac{AK}{BP}\). Do đó:
\(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{DB}=\dfrac{BP}{CK}.\dfrac{CK}{AK}.\dfrac{AK}{BP}=1\), và tới đây ta lại quay về tính như đã trình bày ở trên.

\(D=\dfrac{2x+4}{3x-1}\\ =>3D=\dfrac{6x+12}{3x-1}=\dfrac{2\left(3x-1\right)+14}{3x-1}=2+\dfrac{14}{3x-1}\)
Để 3D nguyên thì : \(\dfrac{14}{3x-1}\in Z\)
\(=>14⋮\left(3x-1\right)\\ =>3x-1\inƯ\left(14\right)=\left\{\pm1;\pm2;\pm7;\pm14\right\}\)
\(=>3x\in\left\{2;0;3;-1;8;-6;15;-13\right\}\\ =>x\in\left\{\dfrac{2}{3};0;1;-\dfrac{1}{3};\dfrac{8}{3};-2;5;-\dfrac{13}{3}\right\}\)
Mà x nguyên \(=>x\in\left\{0;1;-2;5\right\}\)
Do những giá trị trên chỉ là 3D nguyên nên chưa chắc D đã nguyên
Vậy thử lại thay từng giá trị x vào bt D
Kết luận : \(x\in\left\{0;1;-2;5\right\}\)

a, Xét tứ giác MNPB có:
MN//PB (Vì MN//BC và P ϵ BC)
MB//NP (Vì AB//NP và M ϵ AB)
=> Tứ giác MNPB là hbh
b, Ta có:
M là trung điểm AB
MN//BC
=> MN là đường trung bình của tam giác ABC
=> N là trung điểm AC, MN=BC/2 và MN//BC
Xét 2 tam giác AMN và NPC có
AM=NP (Vì AM=BM, BM=NP)
AN=NC
MN=PC ( Vì MN=BC/2, MN=BP)
=> Tam giác AMN = Tam giác NPC (c.c.c)

\(\dfrac{x^2-4}{x^2+3x-10}\)
Để phân thức này xác định thì: \(x^2+3x-10\ne0\)
\(\Rightarrow x^2+5x-2x-10\ne0\)
\(\Rightarrow x\left(x+5\right)-2\left(x+5\right)\ne0\)
\(\Rightarrow\left(x+5\right)\left(x-2\right)\ne0\)
\(\Rightarrow\left\{{}\begin{matrix}x\ne-5\\x\ne2\end{matrix}\right.\)
_________________
Để phân thức này bằng 0 thì:
\(\dfrac{x^2-4}{x^2+3x-10}=0\)
\(\Rightarrow x^2-4=0\)
\(\Rightarrow x^2-2^2=0\)
\(\Rightarrow\left(x+2\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x-2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\left(\text{nhận}\right)\\x=2\left(\text{ }\text{loại}\right)\end{matrix}\right.\)
Vậy chỉ có 1 số x thỏa mãn là: \(x=-2\)

ĐKXĐ: \(x\ne\pm2\)
\(\dfrac{2x^2-x^3}{x^2-4}=\dfrac{x^2\left(2-x\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{-x^2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{-x^2}{x+2}\)
\(---\)
ĐKXĐ: \(x\ne-1\)
\(\dfrac{x+1}{x^3+1}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)

a/
(gt)
=> ME//AF
=> MF//AE
=> AEMF là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có
=> AEMF là HCN (hbh có 1 góc vuông là HCN)
b/
Ta có
MF
Xét tg vuông ABC có
MB=MC (gt); MF//AE => MF//AB
=> AF=BF (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
Ta có
MF=IF (gt)
=> AMCI là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Ta có
=> AMCI là hình thoi (hbh có 2 đường chéo vuông góc là hình thoi)
c/
Ta có
AI//CM (cạnh đối hình thoi) => AI//BC => ABCI là hình thang
Xét tứ giác ABMI có
AI//BC (cmt) => AI//BM
MF//AB (cmt) => MI//AB
=> ABMI là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Để ABCI là hình thang cân => AB=CI (1)
Ta có
AB=MI (cạnh đối hình bình hành ABMI) (2)
AM=CI (cạnh đối hình thoi AMCI) (3)
Từ (1) (2) (3) => AB=AM=MI=CI
Xét tg vuông ABC có
BM=CM (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> AB=AM=BM => tg ABM là tg đều
Để ABCI là hình thang cân thì tg vuông ABC có
d/
Xét tứ giác ADBM có
DE=ME (gt)
AE=BE (gt)
=> ADBM là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AD//BM (cạnh đối hbh) => AD//BC
Ta có
AI//CM (cạnh đối hình thoi AMCI)
=> A;D;I thẳng hàng (từ 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
Ta có
AD=BM (cạnh đối hbh ADBM)
AI=CM (cạnh đối hình thoi AMCI)
BM=CM (gt)
=> AD=AI => A là trung điểm DI
chúc bạn học tốt

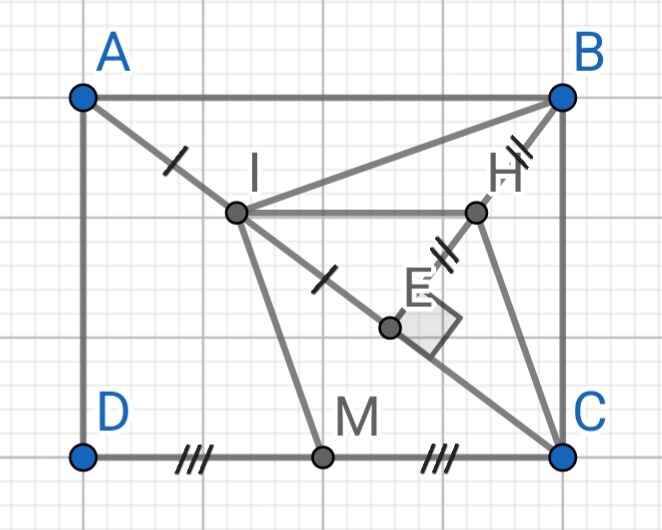
a) Do M là trung điểm của CD (gt)
⇒ CM = DM = CD/2
Do I là trung điểm AE (gt)
H là trung điểm BE (gt)
⇒ HI là đường trung bình của ∆ABE
HI // AB và HI = AB/2 (2)
Do ABCD là hình chữ nhật (gt)
⇒ AB = CD (3)
Từ (1), (2) và (3) ⇒ HI = CM
Do ABCD là hình chữ nhật (gt)
⇒ AB // CD (4)
Từ (2) và (4) ⇒ HI // CD
⇒ HI // CM
Tứ giác CMIH có:
HI // CM (cmt)
HI = CM (cmt)
⇒ CMIH là hình bình hành
⇒ HC // MI
b) Do HC // MI (cmt)
⇒ ∠MIC = ∠ICH (so le trong)
Do HI // MC (cmt)
⇒ ∠HIC = ∠ICM (so le trong)
Do I và H lần lượt là trung điểm của AE và BE (gt)
⇒ AE/BE = AI/BH
Xét hai tam giác vuông: ∆AEB và ∆BEC có:
∠BAE = ∠CBE (cùng phụ ACB)
⇒ ∆AEB ∆BEC (g-g)
⇒ AE/BE = AB/BC
Mà AE/BE = AI/BH (cmt)
⇒ AI/BH = AB/AC
Xét ∆AIB và ∆BHC có:
AI/BH = AB/BC (cmt)
∠BAI = ∠CBH (cùng phụ ACB)
⇒ ∆AIB ∆BHC (g-g)
⇒ ∠ABI = ∠BCH
Do HI // AB (cmt)
⇒ ∠ABI = ∠BIH (so le trong)
⇒ ∠BIH = ∠BCH
Ta có:
∠BIM = ∠BIH + ∠HIC + ∠MIC
= ∠BCH + ∠ICM + ∠ICH
= ∠BCD = 90⁰
Vậy MI ⊥ IB
Gọi N là trung điểm của BE
=> MN là đường trung ình của tam giác ABE
=>MN//AB, MN=1/2 AB
Mà AB=CD và AB//CD
=>MN//CD, MN = 1/2 CD
=> MNCK là hình bình hành
=> NC//MK (1)
Ta có: MN //AB
AB vuông góc với BC
=> MN vuông góc với BC tại E (E thuộc BC)
Tam giác BCM có BE và ME là đường cao và chúng cắt nhau tại N
=> CN vuông góc với BM (2)
Từ (1) và (2) suy ra:
BM vuông góc với MK (đpcm)

Qua B dựng đường thẳng song song với DK và cắt AC tại G
Xét tam giác ADK ta có: AB = BD; BG//DK
⇒ AG = GK (định lý đường trung bình của tam giâc)
⇒ GK = \(\dfrac{1}{2}\) AK (1)
Xét tam giác BCG ta có:
BM = MC; MK // BG
⇒ GK = KC (định lý 1 đường trung bình của tam giác) (2)
Kết hợp (1) và (2) ta có:
KC = \(\dfrac{1}{2}\) AK
⇒ AK = 2KC (đpcm)
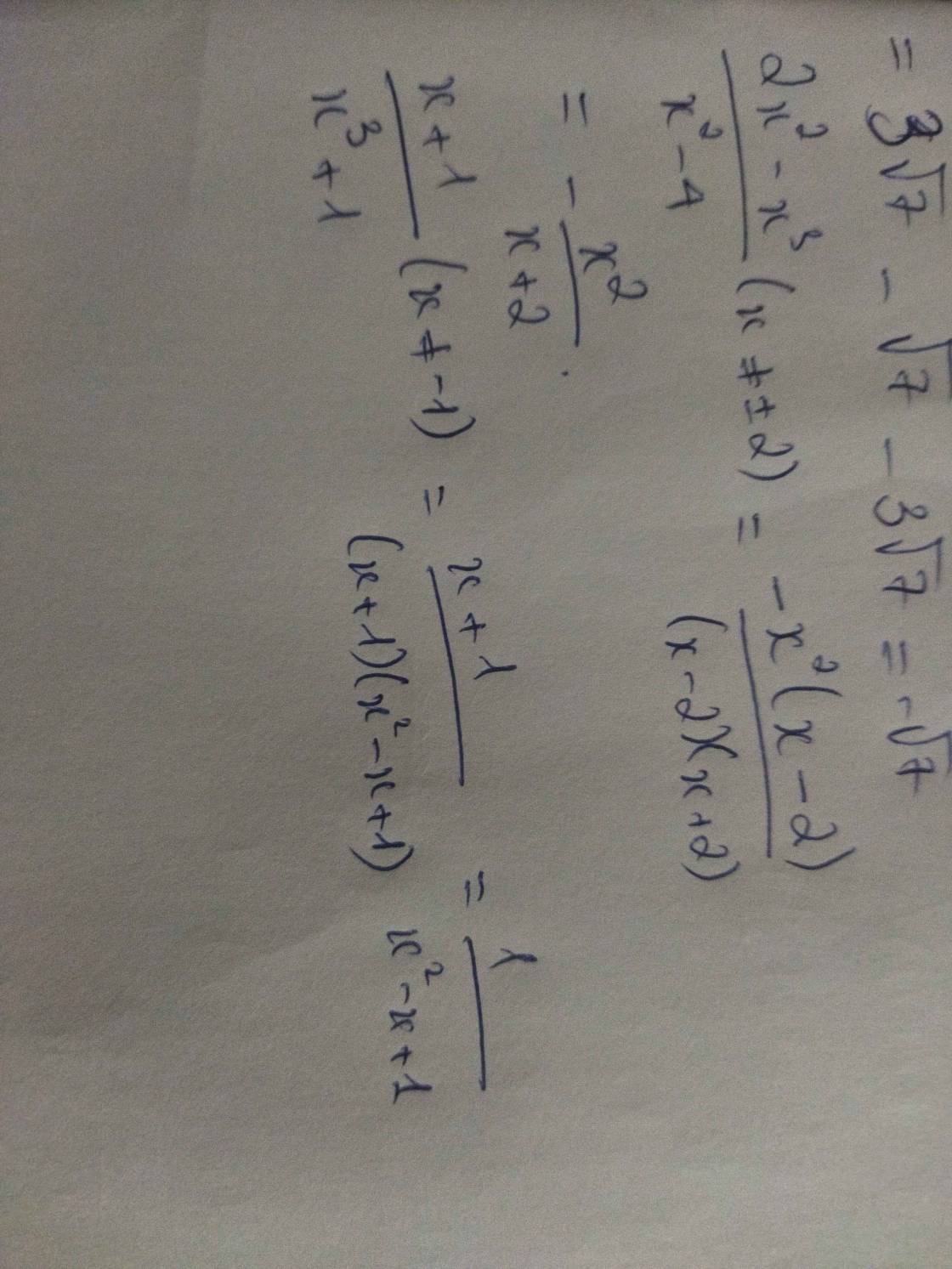
EZ NUB BRO CRY :>
Giả sử : A=(2n+3)2-(2n-1)2
=(4n2+12n+9)-(4n2-4n+1)
=(4n2-4n2)+(12n+4n)+(9-1)
=16n+8
=8(2n+1) ⋮ 8
Vậy A⋮8 (đpcm)
học lại hàng đẳng thức đáng nhớ đi bro :>