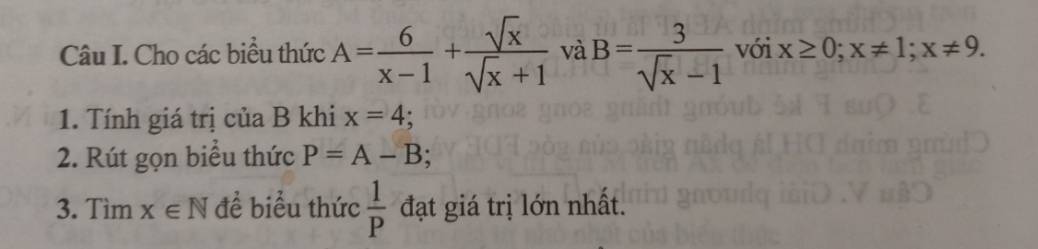(2,5 điểm)
1) Cho hai đường thẳng $y=-x+4\,\left(d_1\right)$ và $y=(\mathrm{m}-2) x+4\,\left(d_2\right)$.
a) Chứng minh rằng không tồn tại giá trị của $\mathrm{m}$ để $\left(d_1\right)$ song song với $\left(d_2\right)$.
b) Gọi giao điểm của $\left(d_1\right)$ với $\left(d_2\right)$ là $P$, giao điểm của $\left(d_1\right)$ với trục $O x$ là $A$. Tìm $\mathrm{m}$ để $\left(d_2\right)$ cắt trục $O x$ tại $B$ sao cho $S_{\triangle P A B}=6$.
2) Một máy bay đang bay ở độ cao $10 \mathrm{~km}$, cách sân bay $100 \mathrm{~km}$ và bắt đầu hạ cánh. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay là một đường thẳng tạo một góc nghiêng so với mặt đất. Tính góc nghiêng đó (làm tròn đến chữ số thập phân thứ nhât).