Cho đại lượng y tỉ lệ thuận với đại lượng x. Biết rằng với hai giá trị x1, x2 của x có x1 – x2 = 1 thì hai giá trị tương ứng y1, y2 của y có y1 – y2 = 4. Khi đó x và y liên hệ với nhau bởi công thức?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số quyển sách cả 3 lớp ủng hộ lần lượt là a ( quyển ), b ( quyển ), c ( quyển ), \(a,b,c\inℕ^∗\)
Ta có: \(\dfrac{a}{5}=\dfrac{b}{6}=\dfrac{c}{8}\) và \(c-a=24\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{5}=\dfrac{b}{6}=\dfrac{c}{8}=\dfrac{c-a}{8-5}=\dfrac{24}{3}=8\)
Do đó:
\(\dfrac{a}{5}=8\Rightarrow a=5.8=40\)
\(\dfrac{b}{6}=8\Rightarrow b=6.8=48\)
\(\dfrac{c}{8}=8\Rightarrow c=8.8=64\)
Vậy số quyển sách cả 3 lớp đã ủng hộ lần lượt là 40 quyển, 48 quyển, 64 quyển.

Ta có: \(2a=5b\Rightarrow\dfrac{a}{5}=\dfrac{b}{2}\Rightarrow\dfrac{3a}{15}=\dfrac{4b}{8}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{3a}{15}=\dfrac{4b}{8}=\dfrac{3a+4b}{15+8}=\dfrac{46}{23}=2\)
Do đó:
\(\dfrac{a}{5}=2\Rightarrow a=5.2=10\)
\(\dfrac{b}{2}=2\Rightarrow b=2.2=4\)
Vậy a = 10; b = 4
\(#WendyDang\)

a; \(\dfrac{x}{6}\) = \(\dfrac{-3}{4}\)
\(x=\dfrac{-3}{4}.6\)
\(x\) = - \(\dfrac{9}{2}\)
Vậy \(x=-\dfrac{9}{2}\)
b; \(\dfrac{5}{x}\) = \(\dfrac{15}{-20}\) (đk \(x\ne0\))
\(x\) = 5 : \(\dfrac{15}{-20}\)
\(x=-\dfrac{20}{3}\)
Vậy \(x=-\dfrac{20}{3}\)
c; \(\dfrac{x+11}{14-x}\) = \(\dfrac{2}{3}\) (đk \(x\ne14\))
3.(\(x+11\)) = 2.(14 - \(x\))
3\(x\) + 33 = 28 - 2\(x\)
3\(x\) + 2\(x\) = 28 - 33
5\(x\) = -5
\(x\) = -1
Vậy \(x\) = -1

a; 5\(x\) - 7 = 3\(x\) + 9
5\(x\) - 3\(x\) = 9 + 7
2\(x\) = 16
\(x\) = 16: 2
\(x\) = 8
Vậy \(x=8\)
b; 1\(\dfrac{3}{4}\)\(x\) + 1\(\dfrac{1}{2}\) = - \(\dfrac{4}{5}\)
\(\dfrac{7}{4}\)\(x\) + \(\dfrac{3}{2}\) = - \(\dfrac{4}{5}\)
\(\dfrac{7}{4}\)\(x\) = - \(\dfrac{4}{5}\) - \(\dfrac{3}{2}\)
\(\dfrac{7}{4}\)\(x\) = - \(\dfrac{23}{10}\)
\(x\) = - \(\dfrac{23}{10}\) : \(\dfrac{7}{4}\)
\(x\) = - \(\dfrac{46}{35}\)
Vậy \(x=-\dfrac{46}{35}\)
c; \(x\) + \(\dfrac{1}{2}\) = 25:23
\(x\) + \(\dfrac{1}{2}\) = 22
\(x\) + \(\dfrac{1}{2}\) = 4
\(x\) = 4 - \(\dfrac{1}{2}\)
\(x\) = \(\dfrac{7}{2}\)
Vậy \(x=\dfrac{7}{2}\)
d; (\(x+\dfrac{1}{2}\))2 = \(\dfrac{4}{25}\)
\(\left[{}\begin{matrix}x+\dfrac{1}{2}=-\dfrac{2}{5}\\x+\dfrac{1}{2}=\dfrac{2}{5}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-\dfrac{2}{5}-\dfrac{1}{2}\\x=-\dfrac{2}{5}+\dfrac{1}{2}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-\dfrac{9}{10}\\x=-\dfrac{1}{10}\end{matrix}\right.\)
vậy \(x\) \(\in\) {- \(\dfrac{9}{10}\); - \(\dfrac{1}{10}\)}

2.(\(\dfrac{1}{4}\) - 3\(x\)) = \(\dfrac{1}{5}\) - 4\(x\)
\(\dfrac{1}{2}\) - 6\(x\) = \(\dfrac{1}{5}\) - 4\(x\)
- 4\(x\) + 6\(x\) =\(\dfrac{1}{2}\) - \(\dfrac{1}{5}\)
2\(x\) = \(\dfrac{3}{10}\)
\(x\) = \(\dfrac{3}{10}\): 2
\(x=\dfrac{3}{20}\)
Vậy \(x=\dfrac{3}{20}\)

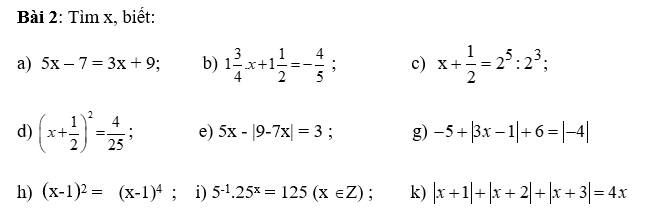
Lời giải:
Gọi $k$ là hệ số tỉ lệ của $y$ so với $x$. Ta có: $y=kx$. Thay $x_1,x_2,y_1,y_2$ thì:
$y_1=kx_1$
$y_2=kx_2$
$\Rightarrow y_1-y_2=kx_1-kx_2$
$\Rightarrow 4=k(x_1-x_2)=k.1=k$
$\Rightarrow y=kx=4x$