7) \(A=1^2-2^2+3^2-4^2+...-2004^2+2005^2\)

\(A=\left(-1\right)\left(1^{ }+2\right)+\left(-1\right)\left(3+4\right)+...+\left(-1\right)\left(2003+2004\right)+2005^2\)

\(A=-\left(1+2+3+...+2004\right)+2005^2\)

\(A=-\dfrac{2004.\left(2004+1\right)}{2}+2005^2\)

\(A=-1002.2005+2005^2\)

\(A=2005\left(2005-1002\right)=2005.1003=2011015\)

8) \(B=\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\left(2^{32}+1\right)-2^{64}\)

\(B=\dfrac{\left(2^2-1\right)}{2-1}\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\left(2^{32}+1\right)-2^{64}\)

\(B=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\left(2^{32}+1\right)-2^{64}\)

\(B=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\left(2^{32}+1\right)-2^{64}\)

\(B=\left(2^{16}-1\right)\left(2^{16}+1\right)\left(2^{32}+1\right)-2^{64}\)

\(B=\left(2^{32}-1\right)\left(2^{32}+1\right)-2^{64}\)

\(B=\left(2^{64}-1\right)-2^{64}\)

\(B=-1\)

\(A=-1^2+2^2-3^2+4^2-...-99^2+100^2\)

\(A=\left(2-1\right).\left(1+2\right)+\left(4-3\right).\left(3+4\right)+...\left(+100-99\right).\left(99+100\right)\)

\(A=1.\left(1+2+3+...+99+100\right)\)

\(A=\dfrac{100.\left(100+1\right)}{2}=50.101=5050\)

Bạn xem lại đề

Ta đặt \(a^2+4b+3=k^2\) 

\(\Leftrightarrow k^2-a^2\equiv3\left[4\right]\)

Mà \(k^2,a^2\equiv0,1\left[4\right]\) nên \(k^2⋮4,a^2\equiv1\left[4\right]\) \(\Rightarrow k⋮2,a\equiv1\left[2\right]\)

Đặt \(k=2l,a=2c+1>b\), ta có \(\left(2c+1\right)^2+4b+3=4l^2\)

\(\Leftrightarrow4c^2+4c+4b+4=4l^2\)

\(\Leftrightarrow c^2+c+1+b=l^2\)

Nếu \(b< c\) thì \(c^2< c^2+c+1+b< c^2+2c+1=\left(c+1\right)^2\), vô lí.

Nếu \(c< b< 2c+1\) thì

\(\left(c+1\right)^2< c^2+c+1+b< c^2+4c+4=\left(c+2\right)^2\), cũng vô lí.

Do vậy, \(c=b\) hay \(a=2b+1\)

Từ đó \(b^2+4a+12=b^2+4\left(2b+1\right)+12\) \(=b^2+8b+16\) \(=\left(b+4\right)^2\) là SCP. Suy ra đpcm.

Đặt \(3p+4=k^2\left(k\ge4\right)\)

\(\Leftrightarrow k^2-4=3p\)

\(\Leftrightarrow\left(k-2\right)\left(k+2\right)=3p\)

Ta thấy \(0< k-2< k+2\) nên có 2TH:

TH1: \(\left\{{}\begin{matrix}k-2=1\\k+2=3p\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}k=3\\3p=5\end{matrix}\right.\), vô lí.

TH2: \(\left\{{}\begin{matrix}k-2=3\\k+2=p\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k=5\\p=7\end{matrix}\right.\), thỏa mãn.

Vậy \(p=7\) là số nguyên tố duy nhất thỏa ycbt.

\(\left(x+1\right)\left(y+1\right)=9\)

\(\Rightarrow xy+x+y+1=9\)

\(\Rightarrow xy+x+y=8\)

\(\Rightarrow x+y=8-xy\left(1\right)\)

\(K=x^2+y^2\)

\(\Rightarrow K=\left(x+y\right)^2-2xy=\left(8-xy\right)^2-2xy\)

\(\Rightarrow K=64-16xy+\left(xy\right)^2-2xy\)

\(\Rightarrow K=\left(xy\right)^2-18xy+64\)

\(\Rightarrow K=\left(xy\right)^2-18xy+81-17\)

\(\Rightarrow K=\left(xy-9\right)^2-17\ge-17\left(\left(xy-9\right)^2\ge0,\forall x;y\right)\)

\(\Rightarrow GTNN\left(K\right)=-17\)

GTNN (K) = -17

PT \(\Leftrightarrow\dfrac{m\left(1-mx\right)+1+mx}{\left(1+mx\right)\left(1-mx\right)}=\dfrac{1}{\left(1-mx\right)\left(1+mx\right)}\)

\(\Rightarrow m-m^2x+1+mx=1\)

\(\Leftrightarrow x\left(m-m^2\right)+m=0\)

Để phương trình vô nghiệm  \(\Leftrightarrow\left\{{}\begin{matrix}m-m^2=0\\m\ne0\end{matrix}\right.\)

\(\Leftrightarrow m=1\)
Vậy \(m=1\)

Số điểm 10 của tổ 1 chiếm số phần của cả lớp là:

\(\dfrac{1}{1+3}=\dfrac{1}{4}\)( cả lớp)

Số điểm 10 của tổ 2 chiếm số phần của cả lớp là:

\(\dfrac{1}{1+4}=\dfrac{1}{5}\)( cả lớp)

Số điểm 10 của tổ 3 chiếm số phần của cả lớp là:

\(\dfrac{1}{5+1}=\dfrac{1}{6}\)( cả lớp)

Số điểm 10 của tổ 4 chiếm số phần của cả lớp là:

\(1-\left(\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}\right)=\dfrac{23}{60}\)( cả lớp)

Số điểm 10 của cả lớp là: 

\(46:\dfrac{23}{60}=120\)( điểm 10)

Vậy số điểm 10 của cả lớp là: \(120\) điểm 10.

Điểm 10 của tổ 1 chiếm số phần điểm 10 của cả lớp là:

\(\dfrac{1}{1+3}=\dfrac{1}{4}\) ( cả lớp )

Điểm 10 của tổ 2 chiến số phần điểm 10 của cả lớp là:

\(\dfrac{1}{4+1}=\dfrac{1}{5}\)  ( cả lớp )

Điểm 10 của tổ 3 chiếm số phần điểm 10 của cả lớp là:

\(\dfrac{1}{5+1}=\dfrac{1}{6}\)  ( cả lớp )

Điểm 10 của tổ 4 chiếm số phần điểm 10 của cả lớp là:

\(1-\left(\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}\right)=\dfrac{23}{60}\)  ( cả lớp )

Cả lớp của tất cả số điểm 10 là:

\(46\div\dfrac{23}{60}=120\)  ( điểm 10 )

Đáp số: \(120\)  điểm 10

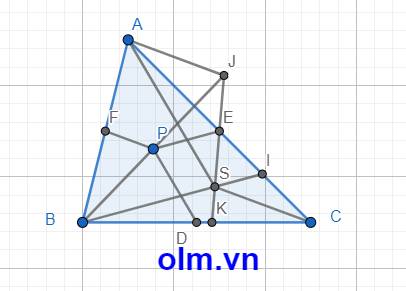
Gọi J là giao điểm của BP và KE; Xét \(\Delta\)BSJ có:

PE // BS; PE = \(\dfrac{1}{2}\) BS 

⇒ PF là đường trung bình của \(\Delta\)BSJ (vì đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy)

⇒ PJ = PB;  EJ = ES (1)

Xét \(\Delta\)ABJ có: AF = FB (gt); PJ = PB  theo (1)

⇒  PF là đường trung bình của \(\Delta\) ABJ (vì đường trung bình của tam giác đi qua trung điểm hai cạnh của tam giác và song song với cạnh còn lại)

 ⇒ PF// AJ  (2) 

Xét tứ giác ASCJ ta có: E là giao điểm hai đường chéo

     AE = EC (gt)

    EJ = ES ( theo (1)

⇒ Tứ giác ASCJ là hình bình hành vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.

⇒ CS // CJ (3)

Kết hợp (2) và(3) ta có:

     CS // PF ( vì trong cùng một mặt phẳng hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau.)

  Kết luận: nếu BS = 2EP thì  CS // PF điều phải chứng minh