Áp dụng hằng đẳng thức, tính giá trị biểu thức:
a.A=x^3-3x^2+3x+1012 tại x=11
b.B=x^3-6x^2+12x-108 tại x=12
c.C=x^3+6x^2y+12xy^2+8y^3 tại x=-2y
d.D=x^3+9x^2+27x+2027 tại x=-23
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
22 tháng 7 2023
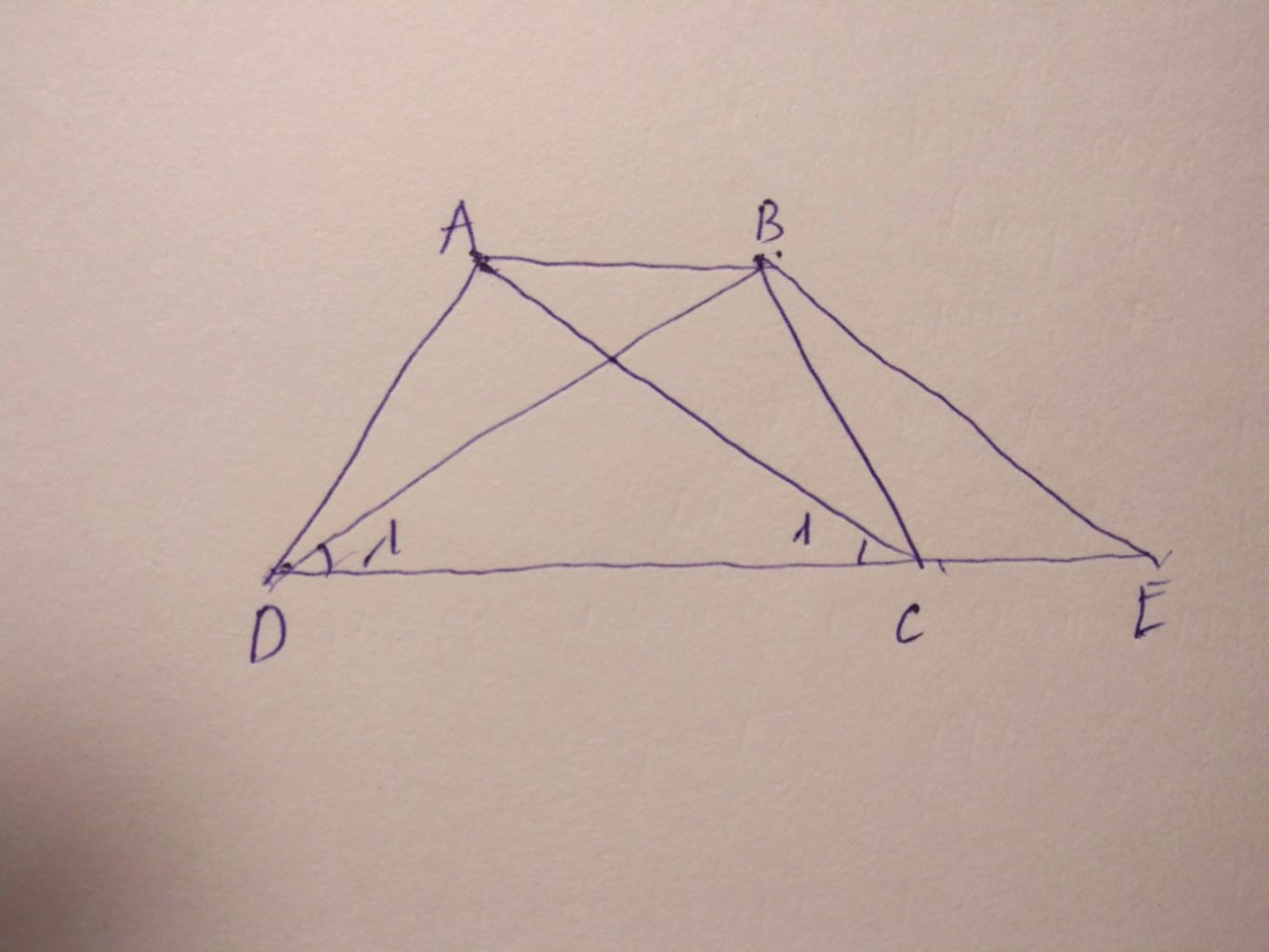
a)Xét ΔACB và ΔEBC,có:
góc ACB=góc EBC(so le trong,AC//BE)
BC chung
góc ABC=góc ECB(so le trong,AB//CE)
⇒ΔACB=ΔEBC(g-c-g)
⇒AC=EB(hai cạnh tương ứng)
Mà AC=BD(gt)
⇒BE=BD
⇒ΔBDE cân tại B
b)Ta có:ΔBDE cân tại B(cmt)
⇒góc BED=góc BDE(2 góc ở đáy)
Mà góc BED=góc ACD(2 góc đồng vị,AC//BE)
⇒góc BDC=góc ACD
Xét ΔACD và ΔBDC,có:
AC=BD(gt)
góc ACD=góc BDC(cmt)
CD chung
⇒ΔACD=ΔBDC(c-g-c)
⇒góc ADC=góc BCD(hai góc tương ứng)
c)Xét hình thang ABCD(AB//CD),có:
góc ADC=góc BCD(cmt)
⇒ABCD là hthang cân
22 tháng 7 2023
a)Xét ΔACB và ΔEBC,có:
góc ACB=góc EBC(so le trong,AC//BE)
BC chung
góc ABC=góc ECB(so le trong,AB//CE)
⇒ΔACB=ΔEBC(g-c-g)
⇒AC=EB(hai cạnh tương ứng)
Mà AC=BD(gt)
⇒BE=BD
⇒ΔBDE cân tại B
b)Ta có:ΔBDE cân tại B(cmt)
⇒góc BED=góc BDE(2 góc ở đáy)
Mà góc BED=góc ACD(2 góc đồng vị,AC//BE)
⇒góc BDC=góc ACD
Xét ΔACD và ΔBDC,có:
AC=BD(gt)
góc ACD=góc BDC(cmt)
CD chung
⇒ΔACD=ΔBDC(c-g-c)
⇒góc ADC=góc BCD(hai góc tương ứng)
c)Xét hình thang ABCD(AB//CD),có:
góc ADC=góc BCD(cmt)
⇒ABCD là hình thang cân
H9
HT.Phong (9A5)
CTVHS
21 tháng 7 2023
\(\left(2x-3\right)^2-\left(x+5\right)\left(4x-1\right)=-9\)
\(\Leftrightarrow4x^2-12x+9-4x^2+x-20x+5=-9\)
\(\Leftrightarrow-31x+14=-9\)
\(\Leftrightarrow-31x=-23\)
\(\Leftrightarrow x=\dfrac{-23}{-31}\)
\(\Leftrightarrow x=\dfrac{23}{31}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
21 tháng 7 2023
\(\Leftrightarrow4x^2-12x+9-4x^2+x-20x-5=-9\)
\(\Leftrightarrow31x=13\Leftrightarrow x=\dfrac{13}{31}\)
TA
2
AH
Akai Haruma
Giáo viên
21 tháng 7 2023
Lời giải:
$=\sqrt{4^2}.\sqrt{5^2}+\sqrt{14^2}: \sqrt{7^2}$
$=4.5+14:7=20+2=22$
21 tháng 7 2023
Xét Δ ADM và Δ BNC ta có :
Góc A = Góc B = 90o (ABCD là HCN)
AD=BC (ABCD là HCN)
AM=BN (đề bài)
⇒ Δ ADM và Δ BNC (cạnh, góc, cạnh)
⇒ Góc ADM = Góc BCN
mà Góc ADM + Góc MDC =90o
Góc BCN + Góc NCD =90o
⇒ Góc MDC = Góc NCD
mà MN song song CD (AB song song CD)
⇒ MNCD là hình thang cân
\(...=A=x^3-3x^2+3x-1+1013\)
\(A=\left(x-1\right)^3+1013=\left(11-1\right)^3+1013=1000+1013=2013\)
\(...B=x^3-6x^2+12x-8-100\)
\(B=\left(x-2\right)^3-100=\left(12-2\right)^3-100=1000-100=900\)
\(...C=\left(x-2y\right)^3=\left(-2y-2y\right)^3=\left(-4y\right)^3=-64y^3\)
\(...D=x^3+9x^2+27x+9+2018\)
\(D=\left(x+3\right)^3+2018=\left(-23+3\right)^3+2018=-8000+2018=-5982\)
a) \(A=x^3-3x^2+3x+1012\)
\(A=x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1+1013\)
\(A=\left(x-1\right)^3+1013\)
Thay x=11 vào A ta có:
\(A=\left(11-1\right)^3+1013=10^3+1013=1000+1013=2013\)
b) \(B=x^3-6x^2+12x-108\)
\(B=x^3-3\cdot2\cdot x^2+3\cdot2^2\cdot x-8-100\)
\(B=\left(x-2\right)^3-100\)
Thay x=12 vào B ta có:
\(B=\left(12-2\right)^3-100=10^3-100=1000-100=900\)
c) \(C=x^3+6x^2y+12xy^2+8y^3\)
\(C=x^3+3\cdot2y\cdot x^2+3\cdot\left(2y\right)^2\cdot x+\left(2y\right)^3\)
\(C=\left(x+2y\right)^3\)
Thay x=-2y vào C ta được:
\(C=\left(-2y+2y\right)^3=0^3=0\)
d) \(D=x^3+9x^2+27x+2027\)
\(D=x^3+3\cdot3\cdot x^2+3\cdot3^2\cdot x+27+2000\)
\(D=\left(x+3\right)^3+2000\)
Thay x=-23 vào D ta có:
\(D=\left(-23+3\right)^3+2000=\left(-20\right)^3+2000=-8000+2000=-6000\)