Chứng minh rằng với mọi số nguyên dương n ta luôn có chia hết cho 25
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Leftrightarrow\dfrac{a}{b}-1=\dfrac{c}{d}-1\)
\(\Leftrightarrow\dfrac{a-b}{b}=\dfrac{c-d}{d}\)

Ta có \(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Leftrightarrow\dfrac{a}{b}+1=\dfrac{c}{d}+1\)
\(\Leftrightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\) (đpcm)

Lời giải:
Ta thấy: $(x-2022)^2\geq 0$ với mọi $x$
$\Rightarrow (x-2022)^2+2\geq 2$
$\Rightarrow \frac{6}{(x-2022)^2+2}\leq 3$ với mọi $x$ (1)
$|y-2023|\geq 0$ với mọi $y$
$\Rightarrow |y-2023|+3\geq 3$ với mọi $y$ (2)
Từ (1); (2) suy ra để $\frac{6}{(x-2022)^2+2}=|y-2023|+3$ thì:
$\frac{6}{(x-2022)^2+2}=|y-2023|+3=3$
$\Rightarrow x-2022=y-2023=0$
$\Leftrightarrow x=2022; y=2023$

Giải thích đoạn:
-5\(x\) - 5 = 3 - 9\(x\)
Chuyển vế đổi dấu ta có:
- 9 \(x\) chuyển sang vế trái ta có: + 9\(x\)
- 5 chuyển sang vế phải ta có: + 5
Vậy -5\(x\) - 5 = 3 - 9\(x\) tương đương với
-5\(x\) + 9\(x\) = 3 + 5
4\(x\) = 8

Hình vẽ này chưa đủ dữ liệu em nhé. Cần phải thêm các yếu tố ví dụ cặp cạnh nào đó hoặc cặp góc nào đó bằng nhau.

Gọi n điểm đó là \(A_1,A_2,...,A_n\) với \(n\ge7\) và giả sử \(A_1,A_2,...,A_7\) thẳng hàng.
Với mỗi điểm \(A_k\left(8\le k\le n\right)\) bất kì, ta có 7 đường thẳng khác nhau được tạo thành là \(A_kA_i\left(i=\overline{1,7}\right)\).
Do có \(n-7\) điểm \(A_k\) khác \(A_i\left(1\le i\le7\right)\) nên số đường thẳng phân biệt được tạo thành là:
\(7\left(n-7\right)+1=7n-48\)
Theo đề bài, ta có:
\(7n-48=211\)
\(\Leftrightarrow7n=259\)
\(\Leftrightarrow n=37\) (nhận)
Vậy \(n=37\)

\(\widehat{M_1}\) = \(\widehat{M_3}\) (hai góc đối đỉnh)
\(\widehat{M_3}\) + \(\widehat{N_1}\) = 1800 (hai góc trong cùng phía)
\(\widehat{M_3}\) = 1800 - \(\widehat{N_1}\)
\(\widehat{M_3}\) = 1800 - 500
\(\widehat{M_3}\) = 1300
⇒ \(\widehat{M_1}\) = 1300
Kết luận: \(\widehat{M_1}\) = 1300

Lời giải:
Giả sử sau $x$ giờ thì ô tô cách M 1 khoảng bằng 1/2 khoảng cách từ xe máy đến M
Có: $AM=MB = AB:2=540:2=270$ (km)
Sau $x$ giờ thì ô tô còn cách $M$: $270-65x$ (km)
Sau $x$ giờ thì xe máy còn cách $M$: $270-40x$ (km)
Có:
$270-65x=\frac{1}{2}(270-40x)$
$\Rightarrow x=3$ (giờ)
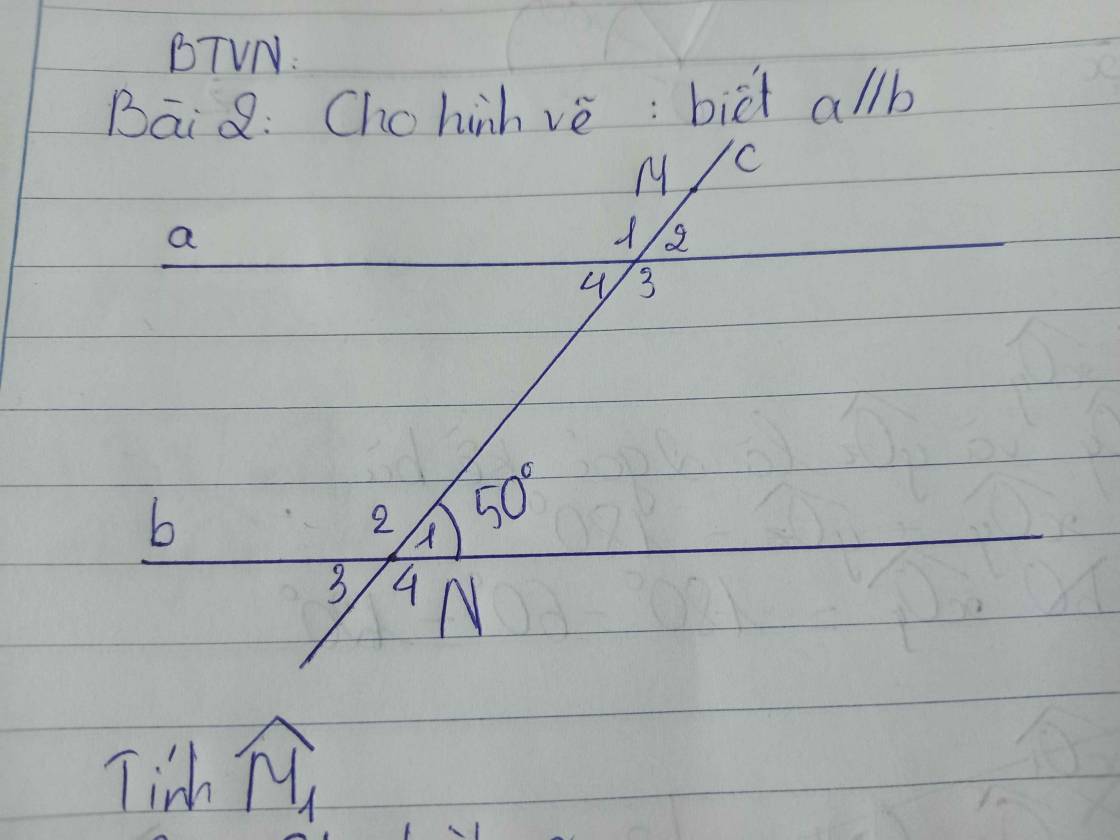
Ta có với n = 1
Thì A = 5n+2 + 3n+2 - 3n - 5n = 51+2 + 31+2 - 31 - 51
A = 53 + 33 - 3 - 5
A = 125 + 27 - 3 - 5
A = (125 - 5) + (27 - 3)
A = 120 + 24
A = 144 Không chia hết cho 25
Vậy việc chứng minh 5n+2 + 3n+2 - 3n - 5n chia hết cho 25 với \(\forall\) n nguyên dương là điều không thể.