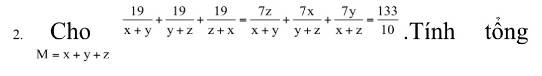Bài 17:

Để $M=\frac{x-5}{11}$ dương thì: $\frac{x-5}{11}>0$

$\Rightarrow x-5>0$

$\Rightarrow x>5$

Để $M=\frac{x-5}{11}$ âm thì $\frac{x-5}{11}<0$

$\Rightarrow x-5<0$

$\Rightarrow x<5$

Để $M=\frac{x-5}{11}=0\Leftrightarrow x-5=0\Leftrightarrow x=5$

-----------------------

Để $N=(x-2)(3-x)>0\Leftrightarrow 2< x< 3$
Để $N=(x-2)(3-x)<0\Leftrightarrow (x-2)(x-3)>0\Leftrightarrow x>3$ hoặc $x<2$

Để $N=(x-2)(3-x)=0\Leftrightarrow x-2=0$ hoặc $3-x=0$

$\Leftrightarrow x=2$ hoặc $x=3$

Bài 18a/

$A=\frac{5-x^2}{x^2+3}=\frac{8-(x^2+3)}{x^2+3}=\frac{8}{x^2+3}-1$
Ta thấy:
$x^2\geq 0$ với mọi $x$

$\Rightarrow x^2+3\geq 3\Rightarrow \frac{8}{x^2+3}\leq \frac{8}{3}$

$\Rightarrow A=\frac{8}{x^2+3}-1\leq \frac{8}{3}-1=\frac{5}{3}$

Vậy $A_{\max}=\frac{5}{3}$. Giá trị này đạt được khi $x^2=0\Leftrightarrow x=0$

Lời giải:

$(a+b+c)(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a})=2007.90$

$\Rightarrow \frac{a}{a+b}+\frac{a}{b+c}+\frac{a}{c+a}+\frac{b}{a+b}+\frac{b}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}+\frac{c}{b+c}+\frac{c}{c+a}=180630$

$\Rightarrow \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}+\frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a}=180630$

$\Rightarrow M+1+1+1=180630$

$\Rightarrow M =180627$

Em ghi đề lại cho chính xác

1\(x\) - (\(x\) - \(\dfrac{1}{3}\)) = \(\dfrac{1}{6}\)

\(x\) - \(x\) + \(\dfrac{1}{3}\)    = \(\dfrac{1}{6}\)

              \(\dfrac{1}{3}\) = \(\dfrac{1}{6}\) (vô lí)

Vậy không có giá trị nào của \(x\) thỏa mãn đề bài

 \(\dfrac{x-1}{-15}\) = - \(\dfrac{60}{x-1}\)

(\(x\) - 1).(\(x\) - 1) = (-60).(-15)

(\(x\) - 1)² = 900

\(\left[{}\begin{matrix}x-1=-30\\x-1=30\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=-29\\x=31\end{matrix}\right.\)

Vậy \(x\in\) {-29; 31}

 ta có:

AB² + AC² = BC²

15² + 20² = 25²

225 + 400 = 625

625 = 25²

=> BC = 25 cm

Từ đó, ta có:

d = √(AB² + AC² - BC²) = √(15² + 20² - 25²) = √(225 + 400 - 625) = √(165) = 12,8 cm

Vậy, khoảng cách từ A đến BC là 12,8 cm.

Cho tam giác ABC,M,N lần lượt là trung điểm AB,AC.Trên tia đối của tia NM xác định điểm P sao cho NP=MN.Chứng minh:

a) CP// AB.       b)MB=CP.          c) BC=2MN

651​<531​+631​+731​+…+202331​<40

165<153+163<153+163+173+…+120233<153+163+173+…+120233+…+120233651​<531​+631​<531​+631​+731​+…+202331​<531​+631​+731​+…+202331​+…+202331​

165<153+163<153+163+173<153+163+173+…+120233651​<531​+631​<531​+631​+731​<531​+631​+731​+…+202331​

Chúng ta có thể thấy rằng:

173+…+120233<165×(20233−73+1)731​+…+202331​<651​×(20233−73+1)

173+…+120233<165×20161731​+…+202331​<651​×20161

173+…+120233<165×311731​+…+202331​<651​×311

173+…+120233<31165731​+…+202331​<65311​

Từ đó, chúng ta có thể kết luận rằng:

165<153+163+173+…+120233<31165651​<531​+631​+731​+…+202331​<65311​

Vì 31165≈4.7846<4065311​≈4.7846<40

=) đpcm

Ta có: \(4x=3y\) hay \(\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{9}=\dfrac{y}{12}\left(1\right)\)

\(4y=3z\) hay \(\dfrac{y}{3}=\dfrac{z}{4}\Rightarrow\dfrac{y}{12}=\dfrac{z}{16}\left(2\right)\)

Từ (1) và (2), suy ra:

\(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{16}\) \(\Rightarrow\dfrac{2x}{18}=\dfrac{y}{12}=\dfrac{z}{16}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{2x}{18}=\dfrac{y}{12}=\dfrac{z}{16}=\dfrac{2x+y-z}{18+12-16}=\dfrac{-14}{14}=-1\)

Do đó:

\(\dfrac{x}{9}=-1\Rightarrow x=9.\left(-1\right)=-9\)

\(\dfrac{y}{12}=-1\Rightarrow y=12.\left(-1\right)=-12\)

\(\dfrac{z}{16}=-1\Rightarrow z=16.\left(-1\right)=-16\)

Vậy x = -9 ; y = -12 ; z = -16

Ta có: \(A=\dfrac{3x-2}{x+2}=\dfrac{3\left(x+2\right)-4}{x+2}=\dfrac{3\left(x+2\right)}{x+2}-\dfrac{4}{x+2}=3-\dfrac{4}{x+2}\)

Để A mang giá trị nguyên khi

 \(4⋮x+2\) hay \(x+2\inƯ\left(4\right)\in\left\{\pm1;\pm2;\pm4\right\}\)

Do đó: 

\(x+2=-1\Rightarrow x=\left(-1\right)-2\Rightarrow x=-3\)

\(x+2=1\Rightarrow x=1-2\Rightarrow x=-1\)

\(x+2=-2\Rightarrow x=\left(-2\right)-2\Rightarrow x=-4\)

\(x+2=2\Rightarrow x=2-2\Rightarrow x=0\)

\(x+2=-4\Rightarrow x=\left(-4\right)-2\Rightarrow x=-6\)

\(x+2=4\Rightarrow x=4-2\Rightarrow x=2\)

Vậy để A là số nguyên khi \(x\in\left\{-3;-1;-4;0;-6;2\right\}\)

Lời giải:
$\frac{19}{x+y}+\frac{19}{y+z}+\frac{19}{z+x}=\frac{133}{10}$

$19(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x})=\frac{133}{10}$

$\Rightarrow \frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}=\frac{133}{10}: 19=\frac{7}{10}(*)$

Lại có:

$\frac{7z}{x+y}+\frac{7x}{y+z}+\frac{7y}{x+z}=\frac{133}{10}$

$\frac{z}{x+y}+\frac{x}{y+z}+\frac{y}{x+z}=\frac{133}{10}:7=\frac{19}{10}$

$\Rightarrow \frac{z}{x+y}+1+\frac{x}{y+z}+1+\frac{y}{x+z}+1=\frac{49}{10}$

$\Rightarrow \frac{x+y+z}{x+y}+\frac{x+y+z}{y+z}+\frac{x+y+z}{x+z}=\frac{49}{10}$

$\Rightarrow (x+y+z)(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{x+z})=\frac{49}{10}$

Sử dụng kq $(*)$ suy ra:

$x+y+z=\frac{49}{10}: \frac{7}{10}=7$