Bài 23: Tính chiều cao của một ngọn núi ( kết quả làm tròn đến hang đơn vị), biết tại hai điểm A, B cách nhau 500m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34 độ và 38 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi x (học sinh) là số học sinh cần tìm (x ∈ ℕ và 280 < x < 350)
Do khi xếp 12 hàng, 15 hàng, 18 hàng đều vừa đủ nên x ⋮ 12; x ⋮ 15; x ⋮ 18
x BC(12; 15; 18)
Ta có:
12 = 2².3
15 = 3.5
18 = 2.3²
BCNN(12; 15; 18) = 2².3².5 = 180
⇒ x ∈ BC(12; 15; 18) = B(180) = {0; 180; 360; ...}
Mà 280 < x < 350 nên không tìm được x thỏa mãn đề bài
Em xem lại số liệu nhé!

42.48 = 42+8 = 410
Vậy 42.48 được ghi kết quả dưới dạng lũy thừa là 410
Chọn A.410

a; 135 + 60 + 365 + 240
= (135 + 365) + (60+ 240)
= 500 + 300
= 800
b; 37.28+ 37.72
= 37.(28 + 72)
= 37.100
= 3700
1290 - 20.(75:73 + 20230)
= 1290 - 20.(72 + 1)
= 1290 - 20.(49 + 1)
= 1290 - 20.50
= 1290 - 1000
= 290

Gọi x (phần thưởng) là số phần thưởng nhiều nhất cô có thể chia (x ∈ ℕ*)
Do cô chia số phần quà từ 240 cuốn vở, 72 cái bút và 168 tập giấy kiểm tra nên x = ƯCLN(240; 72; 168)
Ta có:
240 = 2⁴.3.5
168 = 2³.3.7
72 = 2³.3²
x = ƯCLN(240; 72; 168) = 2³.3 = 24
Vậy số phần thưởng nhiều nhất cô có thể chia là 24 phần thưởng

a)
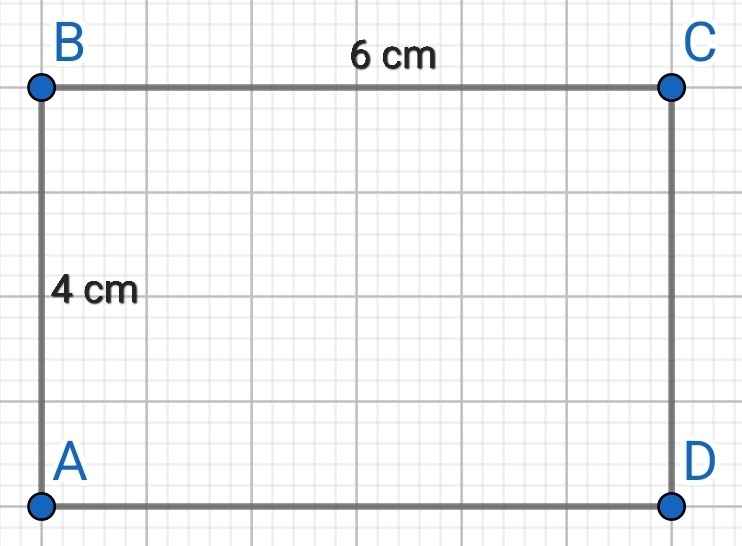
b) Diện tích nền căn phòng:
4.6 = 24 (m²)
40 cm = 0,4 m
Diện tích viên gạch:
0,4.0,4 = 0,16 (m²)
Số viên gạch dùng để lát nền căn phòng:
24 : 0,16 = 150 (viên)
Số tiền bác Nam mua gạch:
150.50000 = 7500000 (đồng)

Vì ƯCLN (a; b) = 8 nên ta có: \(\left\{{}\begin{matrix}a=8d\\b=8k\end{matrix}\right.\)(d;k)=1; d;k \(\in\) N*
tích của a và ba là: 8d.8k = 384 ⇒d.k = 384 : 8 : 8
⇒ d.k = 6; Ư(6) = {1; 2; 3; 6}
Lập bảng ta có:
| d.k | 6 | 6 | 6 | 6 |
| d | 1 | 2 | 3 | 6 |
| k | 6 | 3 | 2 | 1 |
| (d;k) = 1; k;d \(\in\) N* | nhận | nhận | nhận | nhận |
| a = 8d | 8 | 16 | 24 | 48 |
| b = 8k | 48 | 24 | 16 | 8 |
Theo bảng trên ta có: (a; b) = (8; 48); (16; 24); (24; 16); (48; 8)
Kết luận các cặp số tự nhiên thỏa mãn đề bài lần lượt là:
(a; b) = (8; 48); (16; 24); (24; 16); (48 ; 8)
Do ƯCLN(a; b) = 8 nên đặt a = 8m, b = 8n (ƯCLN(m, n) = 1)
Khi đó BCNN(a, b) = BCNN(8m, 8n) = 384
⇒ 8m.n = 384
⇒ mn = 384 : 8 = 48
⇒ mn = 1.48 = 3.16 = 16.3 = 48.1
⇒ (m; n) ∈ {(1; 48); (3; 6); (16; 3); (48; 1)}
⇒ (a; b) ∈ {(8; 384); (24; 128); (128; 24); (384; 8)}