 Cứu be
Cứu be
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


khuya qua rồi ngủ đi. Có giải cũng không nhớ đâu bạn.
Câu a: m = 1, x = 0 và x=2
Câu b ∀mϵ R
vì Δ = 12

Gọi \(x\left(km/h\right)\) là vận tốc xe chạy chậm \(\left(x>0\right)\) và \(y\left(km/h\right)\) là vận tốc của xe đi nhanh \(\left(y>x>0\right)\).
Xét trường hợp đầu tiên:
Sau 5h, xe đi chậm đi được \(5x\left(km\right)\) còn xe đi nhanh đi được \(5y\left(km\right)\).
Vì nếu 2 xe đi ngược chiều và khởi hành cùng một lúc thì sau 5h chúng gặp nhau nên tổng quãng đường của chúng đi được tại thời điểm chúng gặp nhau chính bằng độ dài của quãng đường AB. Do đó, ta có pt \(5x+5y=400\Leftrightarrow x+y=80\) (1)
Từ đây nảy sinh thêm điều kiện \(x,y< 80\)
Xét trường hợp thứ hai:
Trong 40 phút \(=\dfrac{2}{3}h\), xe đi chậm đi được \(\dfrac{2}{3}x\left(km\right)\)
Quãng đường còn lại tại thời điểm xe đi nhanh xuất phát là \(400-\dfrac{2}{3}x\left(km\right)\)
Thời gian từ lúc xe nhanh khởi hành đến lúc gặp nhau là 5h22p - 40p = 4h42p \(=\dfrac{47}{10}\left(h\right)\)
Sau \(\dfrac{47}{10}\left(h\right)\), xe đi chậm đi được \(\dfrac{47}{10}x\left(km\right)\), xe đi nhanh đi được \(\dfrac{47}{10}y\left(km\right)\)
Vì sau 5h22p kể từ lúc xe chậm khởi hành hay 4h42p kể từ lúc xe nhanh khởi hành, chúng gặp nhau, do đó tổng quãng đường 2 xe đi được tại thời điểm chúng gặp nhau chính bằng quãng đường còn lại sau khi xe đi chậm đi trong 40p. Do đó ta có pt \(\dfrac{47}{10}x+\dfrac{47}{10}y=400-\dfrac{2}{3}x\Leftrightarrow\dfrac{161}{30}x+\dfrac{47}{10}y=400\)\(\Leftrightarrow\dfrac{161x+141y}{30}=400\Leftrightarrow161x+141y=12000\) (2)
Từ (1) và (2) ta có hpt \(\left\{{}\begin{matrix}x+y=80\\161x+141y=12000\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=80-x\\161x+141\left(80-x\right)=12000\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=80-x\\161x-141x+11280=12000\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=80-x\\20x=720\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=80-x\\x=36\left(nhận\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=44\left(nhận\right)\\x=36\end{matrix}\right.\)
Vậy vận tốc của xe đi chậm là 36km/h, vận tốc của xe đi nhanh là 44km/h.

Lời giải:
Gọi chiều dài và chiều rộng hcn là $a$ và $b$ (cm)
Theo bài ra ta có:
$a+b=60:2=30$ (cm)
$a=b+6$
$\Rightarrow b+6+b=30$
$\Leftrightarrow b=12$ (cm)
Chiều dài: $a=b+6=12+6=18$ (cm)
 Giúp em với ạ.
Giúp em với ạ.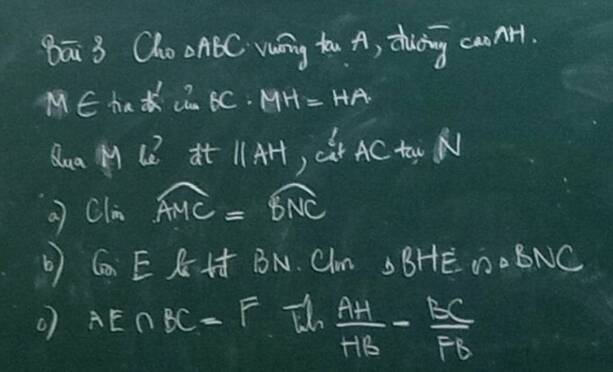
b) Phương trình (1) có hai nghiệm \(x_1,x_2\) do có hệ số \(ac=1.\left(-8\right)=-8< 0\).
Theo định lí Viete ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2-m\\x_1x_2=-8\end{matrix}\right.\)
Ta có:
\(Q=\left(x_1^2-1\right)\left(x_2^2-1\right)=x_1^2x_2^2-\left(x_1^2+x_2^2\right)+1=x_1^2x_2^2-\left(x_1+x_2\right)^2+2x_1x_2+1\)
\(=64-\left(m-2\right)^2-16+1=49-\left(m-2\right)^2\le49\)
Dấu \(=\) xảy ra khi \(m-2=0\Leftrightarrow m=2\).
Vậy \(m=2\) thỏa mãn ycbt.