Cho parabol (P): y = x2 và đường thẳng (d): y = mx - 1 (m khác 0). Tìm các giá trị của m để đường thẳng (d) cắt parabol (P) tại 2 điểm phân biệt có hoành độ x1; x2 thỏa mãn: x2. (x12 + 1) = 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Phương trình có 2 nghiệm phân biệt khi:
\(\Delta'=1-\left(m-1\right)>0\Rightarrow m< 2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(m-1\right)=10\)
\(\Leftrightarrow m=-2\) (thỏa mãn)

Đặt \(\left\{{}\begin{matrix}x+1=a>0\\y+1=b>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=a-1\\y=b-1\end{matrix}\right.\)
Thế vào điều kiện bài toán: \(a-1-2\left(b-1\right)\ge1\Rightarrow a\ge2b\Rightarrow\dfrac{a}{b}\ge2\)
\(A=\dfrac{\left(x+1\right)^2+\left(y+1\right)^2}{\left(x+1\right)\left(y+1\right)}=\dfrac{a^2+b^2}{ab}=\dfrac{a}{b}+\dfrac{b}{a}\)
\(A=\left(\dfrac{a}{4b}+\dfrac{b}{a}\right)+\dfrac{3}{4}.\dfrac{a}{b}\ge2\sqrt{\dfrac{ab}{4ab}}+\dfrac{3}{4}.2=\dfrac{5}{2}\)
\(A_{min}=\dfrac{5}{2}\) khi \(a=2b\) hay \(x=2y+1\)

Phản ứng hoá học:
2CH4 → C2H2 + 3H2
Điều kiện phản ứng
- Nhiệt độ: 1500°C
- Làm lạnh nhanh

Đặt \(\left\{{}\begin{matrix}x+1=a>0\\y+1=b>0\end{matrix}\right.\) \(\Rightarrow\left(a-1\right)-2\left(b-1\right)\ge1\)
\(\Rightarrow a\ge2b\Rightarrow\dfrac{a}{b}\ge2\)
\(A=\dfrac{\left(x+1\right)^2+\left(y+1\right)^2}{\left(x+1\right)\left(y+1\right)}=\dfrac{a^2+b^2}{ab}=\dfrac{a}{b}+\dfrac{b}{a}\)
\(A=\left(\dfrac{a}{4b}+\dfrac{b}{a}\right)+\dfrac{3}{4}.\dfrac{a}{b}\ge2\sqrt{\dfrac{ab}{4ab}}+\dfrac{3}{4}.2=\dfrac{5}{2}\)
\(A_{min}=\dfrac{5}{2}\) khi \(a=2b\) hay \(x+1=2\left(y+1\right)\)

Mình có nghĩ ra cách này mấy bạn xem giúp mình ạ,
Với \(\hept{\begin{cases}x>y\\xy=1\end{cases}}\) ta có:
\(P=\frac{x^2+y^2}{x-y}=\frac{\left(x-y\right)^2+2xy}{x-y}=\frac{\left(x-y\right)^2}{x-y}+\frac{2.1}{x-y}=\left(x-y\right)+\frac{2}{x-y}\)
Áp dụng BĐT Cô - si cho 2 số \(x-y\)và \(\frac{2}{x-y}\)không âm (vì x>y)
\(P\ge2\sqrt{\left(x-y\right).\frac{2}{x-y}}=2\sqrt{2}\)
Vậy minP = \(2\sqrt{2}\)<=> Dấu "=" xảy ra
<=> \(x-y=\frac{2}{x-y}\)
<=> \(\left(x-y\right)^2=2\)
<=> \(x-y=\sqrt{2}\)(vì x - y >0)
Kết hợp với xy = 1 ta có:
\(\hept{\begin{cases}x-y=\sqrt{2}\\xy=1\end{cases}}\)<=> \(\hept{\begin{cases}x+\left(-y\right)=\sqrt{2}=S\\x.\left(-y\right)=-1=P\end{cases}}\)
Xét \(S^2-4P=\left(0\sqrt{2}\right)^2-4.\left(-1\right)=2+4=6>0\)
Vậy x và -y là 2 nghiệm của phương trình:
\(x^2-\sqrt{2}x+\left(-1\right)=0\)
=> \(\orbr{\begin{cases}x_1=\frac{\sqrt{2}+\sqrt{6}}{2}\\x_2=\frac{\sqrt{2}-\sqrt{6}}{2}\end{cases}}\)
Vậy: \(x=\frac{\sqrt{2}+\sqrt{6}}{2}\) và \(y=\frac{-\sqrt{2}+\sqrt{6}}{2}\)
hoặc \(x=\frac{\sqrt{2}-\sqrt{6}}{2}\)và \(y=\frac{-\sqrt{2}-\sqrt{6}}{2}\)

ĐKXĐ : x > 0
\(P=\left(\frac{1}{x+\sqrt{x}}-\frac{1}{\sqrt{x}+1}\right):\frac{\sqrt{x}}{x+2\sqrt{x+1}}\left(x>0\right)\)
\(=\left[\frac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}-\frac{1}{\sqrt{x}+1}\right]:\frac{\sqrt{x}}{\left(\sqrt{x}+1\right)^2}\)
\(=\frac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}.\frac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}\)
\(=\frac{\left(1-\sqrt{x}\right)\left(\sqrt{x}+1\right)}{x}\)
\(=\frac{1-x}{x}\)
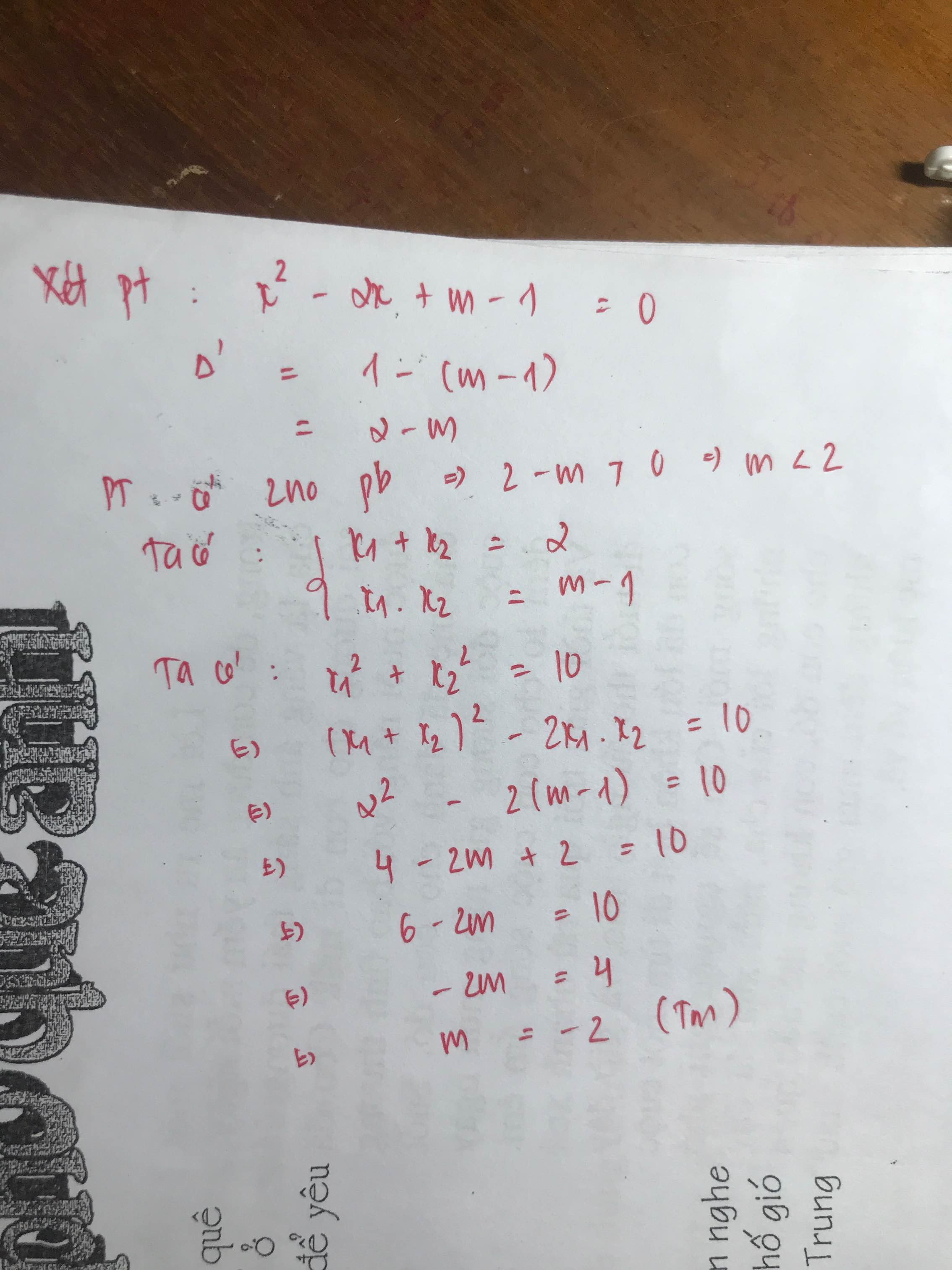
Phương trình hoành độ giao điểm của (P) và (d) là \(x^2=mx-1\)\(\Leftrightarrow x^2-mx+1=0\)(*)
pt (*) có \(\Delta=\left(-m\right)^2-4.1.\left(-1\right)=m^2+4\)
Vì \(m^2+4>0\)nên \(\Delta>0\)hay pt (*) luôn có 2 nghiệm phân biệt, đồng nghĩa với việc (d) luôn cắt (P) tại 2 điểm phân biệt.
Áp dụng hệ thức Vi-ét, ta có \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=1\end{cases}}\)
Như vậy ta có \(x_2\left(x_1^2+1\right)=3\)\(\Leftrightarrow x_2x_1^2+x_2=3\)\(\Leftrightarrow x_1+x_2=3\)\(\Rightarrow m=3\)\
Vậy để (d) cắt (P) tại 2 điểm phân biệt có hoành độ thỏa mãn yêu cầu đề bài thì \(m=3\)