Ta thấy: \(3\left|x+y\right|\ge0\forall x;y\)

              \(10\left|y+\dfrac{2}{3}\right|\ge0\forall y\)

\(\Rightarrow3\left|x+y\right|+10\left|y+\dfrac{2}{3}\right|\ge0\forall x;y\)

Mà: \(3\left|x+y\right|+10\left|y+\dfrac{2}{3}\right|\le0\)

nên: \(\left\{{}\begin{matrix}x+y=0\\y+\dfrac{2}{3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-y\\y=-\dfrac{2}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=-\dfrac{2}{3}\end{matrix}\right.\)

Vậy \(x=\dfrac{2}{3};y=-\dfrac{2}{3}\).

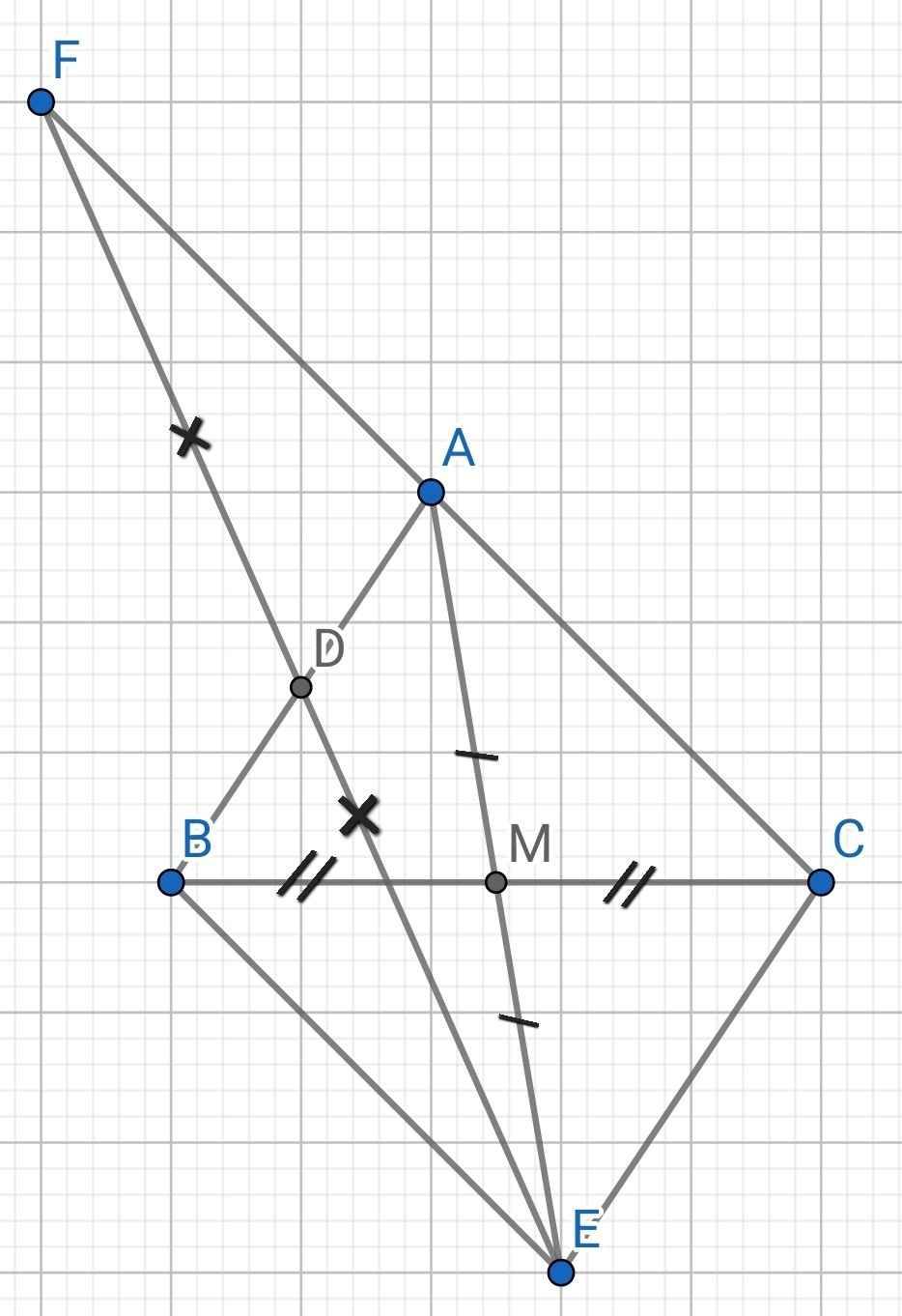 a) Xét ∆AMC và ∆EMB có:

AM = EM (gt)

MC = MB (gt)

∠AMC = ∠EMB (đối đỉnh)

⇒ ∆AMC = ∆EMB (c-g-c)

⇒ AC = BE (hai cạnh tương ứng)

b) Do D là trung điểm AB (gt)

⇒ AD = BD

Xét ∆ADF và ∆BDE có:

AD = BD (cmt)

FD = DE (gt)

∠ADF = ∠BDE (đối đỉnh)

⇒ ∆ADF = ∆BDE (c-g-c)

⇒ AF = BE (hai cạnh tương ứng)

Mà BE = AC (cmt)

⇒ AC = AF

bình phương của 13 là 169

\(13^2=13.13=169\)

Số hữu tỉ nào không nằm giữa -1/3 và 2/3
là số 0

các số <\(\dfrac{-1}{3}\)hoặc >\(\dfrac{2}{3}\)

nếu ko mua vip mỗi ngày được vài phút thôi bạn ạ

O_o

25²⁵ + 5⁴⁹ - 125¹⁶

= (5²)²⁵ + 5⁴⁹ - (5³)¹⁶

= 5⁵⁰ + 5⁴⁹ - 5⁴⁸

= 5⁴⁸.(5² + 5 - 1)

= 5⁴⁸.24